我应该通过哪些措施在MATLAB中设置高斯滤波器的大小？

Question

我正在尝试使用MATLAB学习图像处理,我已阅读有关图像的过滤器.考虑这段代码:

gaussianFilter = fspecial('gaussian', [7, 7], 5)  ,

这构建了一个7行和7列的高斯滤波器矩阵,标准偏差为5.因此,滤波器矩阵的大小为7 x 7.

该矩阵的大小如何在过滤时有效？(这个矩阵有什么作用？)

我应该通过哪些措施在代码中设置滤镜矩阵的大小？

Answer 1

确定高斯滤波器的大小和最终标准偏差的最常见和启发式测量之一是所谓的3-sigma规则.如果从概率还记得,高斯分布的大部分价值中心之间[mu - 3*sigma, mu + 3*sigma],其中mu是分布的均值,sigma是分布的标准偏差.这实际上称为99%置信区间.一个很好的图表如下所示:

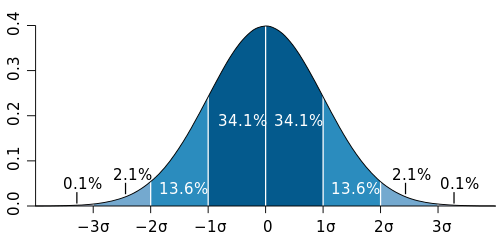
^{资料来源:维基百科}

通过观察[mu - 3*sigma, mu + 3*sigma],大多数变化可以包含在高斯分布下面的总面积的99%内.作为旁注,介于两者之间[mu - 2*sigma, mu + 2*sigma],这占据了总面积的大约95%,最后 [mu - sigma, mu + sigma]覆盖了总面积的约68%.

因此,人们通常会做的是查看图像并找出最小的特征.它们测量特征的宽度或高度,并确保特征的宽度/高度/跨度符合99%置信区间.测量横跨给我们的总宽度6*sigma.但是,因为我们处理离散域,所以我们也需要适应高斯中心.因此,您需要确保总宽度为: 2 * floor(3*sigma) + 1.因此,您需要做的是找出您想要的宽度.一旦你这样做,你就可以弄清楚sigma满足这个宽度需要什么.举个例子,假设我们最小的特征的宽度是19.然后你会弄明白你sigma的意思:

19 = 2*floor(3*sigma) + 1
19 = 6*sigma + 1
18 = 6*sigma
sigma = 3

因此,您可以像这样创建高斯内核:

h = fspecial('gaussian', [19 19], 3);

如果你想玩掩模尺寸,只需使用上面的等式来操纵和解决sigma每次.现在回答关于大小的问题,这是一个低通滤波器.因此,增加矩阵的大小实际上会增加LPF的效果.随着图像尺寸的增加,图像会逐渐变得模糊.玩大小,看看你得到了什么.如果在尝试此操作时没有任何特定图像,则可以使用MATLAB中的任何内置图像.因此,请尝试执行以下操作:

%// Read in the image - Part of MATLAB path
im = imread('cameraman.tif');

%// Determine widths and standard deviations
width1 = 3; sigma1 = (width1-1) / 6;
width2 = 7; sigma2 = (width2-1) / 6;
width3 = 13; sigma3 = (width3-1) / 6;
width4 = 19; sigma4 = (width4-1) / 6;

%// Create Gaussian kernels
h1 = fspecial('gaussian', [width1 width1], sigma1);
h2 = fspecial('gaussian', [width2 width2], sigma2);
h3 = fspecial('gaussian', [width3 width3], sigma3);
h4 = fspecial('gaussian', [width4 width4], sigma4);

%// Filter the image using each kernel
out1 = imfilter(im, h1, 'replicate');
out2 = imfilter(im, h2, 'replicate');
out3 = imfilter(im, h3, 'replicate');
out4 = imfilter(im, h4, 'replicate');

%// Display them all on a figure
figure;
subplot(2,2,1);
imshow(out1);
title(['Width = 3']);
subplot(2,2,2);
imshow(out2);
title(['Width = 7']);
subplot(2,2,3);
imshow(out3);
title(['Width = 13']);
subplot(2,2,4);
imshow(out4);
title(['Width = 19']);

您将获得以下输出: