小编VcS*_*Jen的帖子

问题
我需要将尺寸为n×m的矩形放入尺寸为N×M的矩阵的自由区域中,其中N=n*2-1,M=m*2-1.矩阵单元被认为是免费的,如果它是true,并被占用false.true由于矩形和矩阵的大小,中心单元始终是,并且始终位于矩形内部.

附加要求是矩形和中心单元的左上角之间的距离必须尽可能小.

带n=8和的示例m=5:

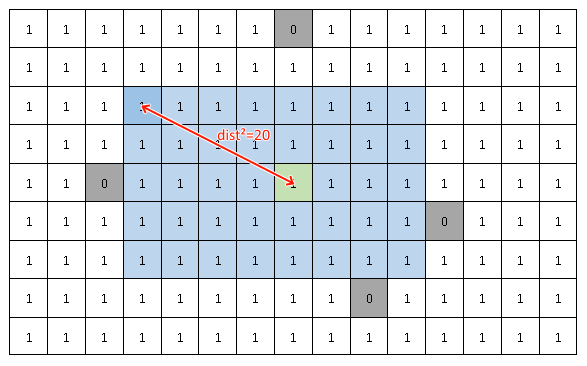
灰色细胞占据,绿色 - 中心细胞,蓝色细胞 - 解矩形,红线 - 矩形左上角和中心细胞之间的距离.

尝试
暴力解决方案将具有O(N×M×n×m)时间复杂度,这不是非常优化的.如果我预处理矩阵,我可以消除某些单元格中的计算,但这仍然会花费太多时间.

最初我认为我可以采取Max Rectangle问题并且只是将条件从max修改为需要,但是它进入了死胡同(我需要列出直方图中的所有矩形,我不知道如何).然后我认为它就像打包问题,但我能找到的只是它的版本,最初是完全空的空间和多个矩形,这不适用于这个问题.

上下文
在过去,当用户点击网格时,我的程序会放置矩形,左上角与点击点重合,如果它是空的,如果它已经占用了矩形所在的单元格则会失败.我决定修改这种行为,而不是失败,找到最合适的矩形位置,同时仍然包含一个点击点.在上面的矩阵pic中,单击点是绿色单元格,矩阵大小表示矩形的所有可能位置.

PS如果可能的话,我更喜欢真实的语言示例而不是伪代码.我的程序是用Java编写的,但任何语言都可以.