标签: np-complete

NP,NP-Complete和NP-Hard有什么区别？

我知道网上有很多资源.我想阅读你的解释,原因是它们可能与那些不同,或者有些东西我不知道.

什么是NP完全问题？为什么它是计算机科学中如此重要的话题？

P = NP的问题可能是所有计算机科学中最着名的问题.这是什么意思？为什么它如此有趣？

哦,为了额外的功劳,请发表声明的真相或虚假证明.:)

问题/漫画有问题:http://xkcd.com/287/

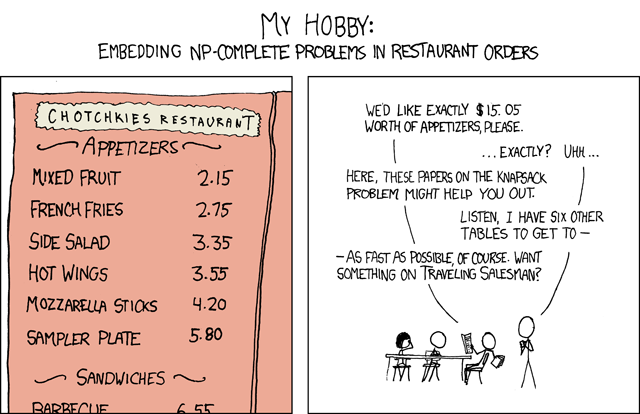
我不确定这是最好的方法,但这是我到目前为止所提出的.我正在使用CFML,但任何人都应该可读.

<cffunction name="testCombo" returntype="boolean">
    <cfargument name="currentCombo" type="string" required="true" />
    <cfargument name="currentTotal" type="numeric" required="true" />
    <cfargument name="apps" type="array" required="true" />

    <cfset var a = 0 />
    <cfset var found = false />

    <cfloop from="1" to="#arrayLen(arguments.apps)#" index="a">
        <cfset arguments.currentCombo = listAppend(arguments.currentCombo, arguments.apps[a].name) />
        <cfset arguments.currentTotal = arguments.currentTotal + arguments.apps[a].cost />
        <cfif arguments.currentTotal eq 15.05>
            <!--- print current combo --->
            <cfoutput><strong>#arguments.currentCombo# = 15.05</strong></cfoutput><br />
            <cfreturn true />
        <cfelseif arguments.currentTotal gt 15.05>
            <cfoutput>#arguments.currentCombo# > 15.05 (aborting)</cfoutput><br />
            <cfreturn false /> …

首先,让我说,这不是功课(我是一个A-Level的学生,这是没有接近我们解决问题(这是路难)),但更多的问题,我想苏斯出来的改善我的编程逻辑.

我想到了一个有一个随机整数数组的场景,比如说10个整数.用户将输入他想要计数的数字,算法将尝试计算出该总和所需的数字.例如,如果我想从这个整数数组中得到总和44:

myIntegers = array(1, 5, 9, 3, 7, 12, 36, 22, 19, 63);

输出将是:

36 + 3 + 5 = 44

或类似的规定.我希望我能说清楚.作为一个额外的好处,我想让算法选择尽可能少的数字来产生所需的总和,或者如果不能用所提供的数字进行求和则给出错误.

我想过使用递归和遍历数组,反复添加数字直到满足或超过总和.但是我无法理解的是,如果算法超过总和并且需要选择从阵列中选择的数字,该怎么办.

我不是在寻找完整的代码,也不是一个完整的算法,我只是希望你对我应该如何处理这个问题提出意见,也许还会分享一些提示或其他内容.我今晚可能会开始研究这个问题.:P

正如我所说,不是功课.只是我想要做一些更先进的事情.

感谢您提供的任何帮助.:)

来自NP-Complete的维基百科条目:

"证明一些新问题是NP完全的最简单的方法是首先证明它是在NP中,然后减少一些已知的NP完全问题"

我很确定我理解这一点:如果我有问题,我可以证明它是NP-Complete如果我:

1. 表明它在NP中(可以在非确定性图灵机上的多项式时间内验证问题的解决方案)

2. 表明已知为NP-Complete的问题可以"减少"到新问题

所以,我的问题是,第一个NP完全问题"被证明"是NP完全的吗？同时,已知NP完全问题的集合必须为零,这将使得在上述过程中不可能采用步骤2.

这让我觉得有一种不同的证明方法,我不知道.由于缺少已知的多项式时间解决方案,或者可能由于缺少已知的多项式时间解而对某些问题"假设"整个NP完全属性.(实际上,写完这篇文章后,如果是这样的话,我不会感到惊讶,但无论如何我都喜欢一些古茹反馈).

有一个数字列表.

该列表将分为2个相等大小的列表,总和之间的差异最小.必须打印总和.

#Example:
>>>que = [2,3,10,5,8,9,7,3,5,2]
>>>make_teams(que)
27 27

在某些情况下,以下代码算法是否存在错误？

我如何优化和/或pythonize这个？

def make_teams(que):
    que.sort()
    if len(que)%2: que.insert(0,0)
    t1,t2 = [],[]
    while que:
    val = (que.pop(), que.pop())
    if sum(t1)>sum(t2):
        t2.append(val[0])
        t1.append(val[1])
    else:
        t1.append(val[0])
        t2.append(val[1])
    print min(sum(t1),sum(t2)), max(sum(t1),sum(t2)), "\n"

问题来自http://www.codechef.com/problems/TEAMSEL/

这个问题出现在现实世界中,但我已将其翻译成更通用的"类似教科书"的表述.我怀疑它是NP,但我特别感兴趣的是知道它是否有名字或者是众所周知的,因为我认为我不能成为第一个遇到它的人.;-)

想象一下,有N位客人参加聚会.每位客人都可以将他/她的"招牌菜"带到聚会上,或者什么都不带.每位客人都喜欢或讨厌其他客人可能带来的每道菜(由于他们都是老朋友,所以这是事先知道的!),但他们都喜欢自己的菜肴.

有没有一个确定性的算法,不需要指数时间来找到满足约束的最小菜肴,所有客人都会找到至少一个他们喜欢的菜？我说"最小",但实际上可能有多种解决方案,如果可能的话我想知道它们.

或者,以更抽象的方式,想象一个方形矩阵,其中所有元素都是0或1,并且所有对角元素都是1.什么是最小的行集合,使得每个行的总和(或二进制OR)设置没有零？(行将是菜肴,列将是客人,1意味着客人喜欢菜,对角元素是1,因为每个人都喜欢他们自己的菜.)

这可以推广到非平方矩阵,或者通过去除diagonal = 1规则(尽管后者保证总是存在至少一个解).但我现在不关心这些案件......

我已经有一个程序通过详尽的搜索来解决它,并且对于大约20的N来说足够快,但它需要指数时间.我想我可能需要重复使用随机算法来找到更大的N值的足够好的解决方案.

添加

哇,谢谢你的快速回答!"设置封面",这就是我要找的名字.:)

今天有一个关于SO 的问题,作者在采访中遇到了NP完全问题,他显然没有被告知这是一个问题.

问这些问题的目的是什么？在询问这些事情时,面试官会有什么样的行为？证明？有用的启发式方法？如果它不是每个人都应该知道的众所周知的NP完全问题,那么问一个人是否合法？(这里有很多)

我知道有一些调度问题是NP-hard/NP-complete ...但是,没有一个以这样的方式表明这种情况也是NP.

如果您有一组约束到startAfter,startBy和duration的任务,所有尝试使用单个资源 ...您是否可以解决计划或确定无法在没有详尽搜索的情况下解决它？

如果答案是"对不起,但这是NP完全",那么最好的启发式(s？)是什么,并且有办法减少a)解决时间表和b)识别无法解决的时间时间表.

我通过实现"最小窗口优先"启发式的递归实现了(在prolog中)一个基本的冲突解决目标.这实际上很快找到了解决方案,但在查找无效的计划时非常慢.有办法克服这个问题吗？

耶和复合问题!