标签: graph-theory

任何人都可以告诉我,在网络上我可以找到一个解释Bron-Kerbosch算法的集团发现或解释它是如何工作的？

我知道它发表在"算法457:找到无向图的所有派系"一书中,但我找不到能描述算法的自由源.

我不需要算法的源代码,我需要解释它是如何工作的.

给定带有加权边的有向图,可以使用什么算法给出具有最小权重的子图,但允许从图中的任何顶点移动到任何其他顶点(假设任何两个顶点之间的路径始终存在) .

这样的算法存在吗？

我不想在大学里接受比我更多的数学,图论理论课程不是必修课,而是由CS部门"推荐".对于程序员来说,学习图论是否值得？

这是与动态编程相关的另一算法问题

这是问题所在:

找到给定矩阵的最小总和,以便在每行和每列中选择一个

例如 :

3 4 2

8 9 1

7 9 5

最小的一个:4 + 1 + 7

我认为解决方案是网络流量(最大流量/最小切割量),但我认为它不应该像它那样难

我的解决方案:单独列出[column],column1,column2 ... column n

然后开始点(S) - > column1 - > column2 - > ... - >列n - >(E)终点并实现最大流量/分钟切割

我是SO和postgres的新手所以请原谅我的无知.尝试使用类似于本文中的解决方案在postgres中获取图表的集群在PostgreSQL中查找集群给定节点

唯一的区别是我的id是一个UUID,我使用varchar(255)来存储这个id

当我尝试运行查询时,我收到以下错误(但不知道如何投射):

ERROR: recursive query "search_graph" column 1 has type character varying(255)[] in non-recursive term but type character varying[] overall

SQL状态:42804提示:将非递归项的输出强制转换为正确的类型.性格:81

我的代码(与上一篇文章基本相同):

WITH RECURSIVE search_graph(path, last_profile1, last_profile2) AS (
SELECT ARRAY[id], id, id
FROM node WHERE id = '408d6b12-d03e-42c2-a2a7-066b3c060a0b'
UNION ALL
SELECT sg.path || m.toid || m.fromid, m.fromid, m.toid
FROM search_graph sg
JOIN rel m
ON (m.fromid = sg.last_profile2 AND NOT sg.path @> ARRAY[m.toid]) 
   OR (m.toid = sg.last_profile1 AND NOT sg.path @> ARRAY[m.fromid])
)

 SELECT DISTINCT unnest(path) FROM …

我正在寻找一种方法,从节点和度数的所有强连接有向图(没有自循环)的空间均匀地采样.nk=(k_1,...,k_n), 1 <= k_i <= n-1

输入

• n,节点数量
• k = (k_1,...,k_n),其中k_i =进入节点的有向边数i(度数)

产量

• 具有n给定度数的节点(没有自循环)的强连接有向图,k_1,...,k_n其中每个可能的这样的图以相同的概率返回.

我特别感兴趣的n是大而k_i小的情况,因此简单地创建图形并检查强连通性是不可行的,因为概率基本上为零.

我浏览了各种各样的论文和方法,但找不到任何可以解决这个问题的方法.

如果我们的目标时间复杂度是O(| V |*| E |)或O(V ^ 3)等,则该问题具有简单的解决方案.但是,我的教授最近给了我们一个问题陈述的任务:

设G =(V,E)为连通无向图.编写一个算法,确定G是否包含O(| V | + | E |)中的三角形.

在这一点上,我很难过.维基百科说:

可以测试具有m个边的图在时间O(m ^ 1.41)中是否是无三角形的.

除了在Quantum计算机上运行的算法之外,没有提到更快算法的可能性.之后我开始诉诸更好的消息来源.关于Math.SE的一个问题将我与本文联系起来说:

已知用于查找和计数三角形的最快算法依赖于快速矩阵乘积并且具有O(n ^ω)时间复杂度,其中ω<2.376是快速矩阵乘积指数.

而这就是我开始意识到的可能,我们被欺骗了解决一个未解决的问题!那个卑鄙的教授!

但是,我仍然有点怀疑.该文件称"寻找和计算".这相当于我试图解决的问题吗？

TL; DR:我被愚弄了,还是我忽视了一些如此微不足道的事情？

通过迭代修剪顶点来计算图的k核是很容易的.但是,对于我的应用程序,我希望能够将顶点添加到起始图并获得更新的核心,而无需从头开始重新计算整个k-core.是否有可靠的算法可以利用先前迭代所做的工作？

对于好奇的人来说,k-core被用作集团发现算法中的预处理阶段.任何大小为5的小团体都保证是图形的4核心的一部分.在我的数据集中,4核比整个图要小得多,所以从那里强制它可能是易处理的.增量添加顶点使算法可以使用尽可能小的数据集.我的顶点集是无限的和有序的(素数),但我只关心编号最小的集团.

编辑:

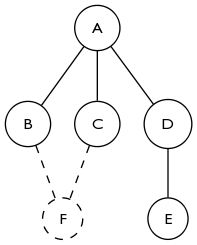
基于akappa的答案更多地考虑它,检测循环的创建确实很关键.在下图中,在添加F之前,2核是空的.添加F不会改变A的程度,但它仍然将A添加到2核.扩展它很容易看到关闭任何大小的循环会导致所有顶点同时加入2核.

添加顶点会对任意距离之外的顶点的核心性产生影响,但这可能会过多地关注最坏情况的行为.

想象一下Git背后的数据结构.它就像一个有条理的持久性数据结构,除了使用散列引用而不是传统的指针.

我需要Git的数据结构,除了没有任何工作树和索引的东西.并且将有数百万个分支机构,每个分支机构跟踪少数其他本地分支机构.提交和合并将在不同的线程上每分钟发生几千次.拉动会每秒发生一次.

在libgit2和jgit之间我可以使用Git的数据存储子系统.

但我使用合适的工具吗？是否有一个具有git功能的数据库,但更快/更多并发/可扩展/更少阻抗不匹配？内存缓存写入非常有用.

任务:

一个协作编辑的游戏.每个玩家都有自己的分支,他们对游戏世界所做的每一项改变都只适用于他们的版本.可信用户将更改合并回"主"分支.数据和源代码通常捆绑在一起,需要相同的分支和合并功能.

我正在使用 networkx 来解决最短路径问题。我主要使用shortest_path。我想知道，使用当前版本的 networkx，是否可以限制最短路径计算？

下面的示例生成了 A 和 G 之间的这两条最短路径：

左边的图片显示了最小化“长度”属性时的最佳路线，右边的图片显示了最小化“高度”属性时的最佳路线。

如果我们计算这些路线的统计数据，我们会得到：

Best route by length: ['A', 'B', 'E', 'F', 'D', 'G']
Best route by height: ['A', 'C', 'E', 'G']
Stats best routes: {
                   'by_length': {'length': 13.7, 'height': 373.0}, 
                   'by_height': {'length': 24.8, 'height': 115.0}
                   }

有没有办法在计算最短路径时添加约束？（例如，通过最小化长度属性来计算最短路径，但同时保持height<300

计算图网络的代码：

Best route by length: ['A', 'B', 'E', 'F', 'D', 'G']
Best route by height: ['A', 'C', 'E', 'G']
Stats best routes: {
                   'by_length': {'length': 13.7, 'height': 373.0}, 
                   'by_height': {'length': 24.8, 'height': …