我正在研究 WGAN，并希望实现 WGAN-GP。

在其原始论文中，由于 1-Lipschitiz 约束，WGAN-GP 是通过梯度惩罚来实现的。但是像 Keras 这样的包可以将梯度范数限制为 1（根据定义，这相当于 1-Lipschitiz 约束），那么为什么我们要费心去惩罚梯度呢？为什么我们不直接裁剪渐变呢？

我正在尝试对葡萄酒数据集实施多元线性回归。但是当我将 Pytorch 的结果与 Python 的临时代码进行比较时，损失并不相同。

我的暂存代码：

功能：

def yinfer(X, beta):
  return beta[0] + np.dot(X,beta[1:]) 

def cost(X, Y, beta):
  sum = 0
  m = len(Y)
  for i in range(m): 
    sum = sum + ( yinfer(X[i],beta) - Y[i])*(yinfer(X[i],beta) - Y[i])
  return  sum/(1.0*m)

主要代码：

alpha = 0.005
b=[0,0.04086357 ,-0.02831656  ,0.09622949 ,-0.15162516  ,0.60188454  ,0.47528714,
  -0.6066466  ,-0.22995654 ,-0.58388734  ,0.20954669 ,-0.67851365]
beta = np.array(b)
print(beta)
iterations = 1000
arr_cost = np.zeros((iterations,2))
m = len(Y)
temp_beta = np.zeros(12)
for i in range(iterations):
  for k in range(m): 
        temp_beta[0] …

问题

在 CS231使用反向传播计算解析梯度中，它首先实现了 Softmax 分类器，将 (softmax + log loss) 的梯度除以批量大小（在训练中前向成本计算和反向传播的循环中使用的数据数量） ）。

请帮助我理解为什么需要除以批量大小。

获得梯度的链式法则应该如下。我应该在哪里合并该部门？

• Softmax损失函数的导数

代码

N = 100 # number of points per class
D = 2 # dimensionality
K = 3 # number of classes
X = np.zeros((N*K,D)) # data matrix (each row = single example)
y = np.zeros(N*K, dtype='uint8') # class labels

#Train a Linear Classifier

# initialize parameters randomly
W = 0.01 * np.random.randn(D,K)
b = np.zeros((1,K))

# some hyperparameters
step_size = 1e-0
reg = …

我正在学习机器学习课程。我有一个简单的线性回归 (LR) 问题来帮助我习惯 TensorFlow。在LR问题是找到参数a和b使得Y = a*X + b近似于(x, y)点云（我生成自己为简单起见）。

我正在使用“固定步长梯度下降（FSSGD）”解决这个 LR 问题。我使用 TensorFlow 实现了它并且它有效，但我注意到它在 GPU 和 CPU 上都非常慢。因为我很好奇，所以我自己在 Python/NumPy 中实现了 FSSGD，正如预期的那样，它运行得更快，大约：

• 比 TF@CPU 快 10 倍
• 比 TF@GPU 快 20 倍

如果 TensorFlow 这么慢，我无法想象有这么多人在使用这个框架。所以我一定是做错了什么。任何人都可以帮助我，以便我可以加速我的 TensorFlow 实现。

我对 CPU 和 GPU 性能之间的差异不感兴趣。提供这两个性能指标只是为了完整性和说明。 我对为什么我的 TensorFlow 实现比原始 Python/NumPy 实现慢得多感兴趣。

作为参考，我在下面添加了我的代码。

• 剥离为最小（但完全有效）的示例。
• 使用Python v3.7.9 x64.
• 用tensorflow-gpu==1.15现在（因为课程使用TensorFlow V1）
• 经测试可在 Spyder 和 PyCharm 中运行。

我使用 TensorFlow 的 FSSGD 实现（执行时间大约 40 秒 @CPU 到 80 …

我正在尝试编写一个代码，使用梯度下降返回岭回归的参数。岭回归定义为

其中，L 是损失（或成本）函数。w 是损失函数的参数（同化 b）。x 是数据点。y 是每个向量 x 的标签。lambda 是正则化常数。b 是截距参数（同化为 w）。所以，L(w,b) = 数字

我应该实现的梯度下降算法如下所示：

其中\xe2\x88\x87\是L相对于w的梯度。\xce\xb7

是步长。t 是时间或迭代计数器。

我的代码：

def ridge_regression_GD(x,y,C):\n    x=np.insert(x,0,1,axis=1) # adding a feature 1 to x at beggining nxd+1\n    w=np.zeros(len(x[0,:])) # d+1\n    t=0\n    eta=1\n    summ = np.zeros(1)\n    grad = np.zeros(1)\n    losses = np.array([0])\n    loss_stry = 0\n    while eta > 2**-30:\n        for i in range(0,len(y)): # here we calculate the summation for all rows for loss and gradient\n            summ=summ+((y[i,]-np.dot(w,x[i,]))*x[i,])\n …

我正在研究“使用 fastai 和 Pytorch 为编码人员进行深度学习”。第 4 章通过一个简单的例子介绍了 PyTorch 库中的 autograd 函数。

x = tensor([3.,4.,10.]).requires_grad_()
def f(q): return sum(q**2)
y = f(x)
y.backward()

我的问题归结为：y = f(x)is的结果tensor(125., grad_fn=AddBackward0)，但这到底意味着什么？为什么我要将三个完全不同的输入值相加？

我知道.backward()在这种情况下使用是在这种情况下的简写.backward(tensor[1.,1.,1.])，但我没有看到在列表中对 3 个不相关的数字求和如何帮助获得任何东西的梯度。我不明白什么？

_{我不是在这里寻找研究生级别的解释。我正在使用的这本书的副标题是没有博士学位的人工智能应用程序。我在学校的渐变经验是我应该恢复一个功能，但我知道 Autograd 不是这种情况。这个简短示例的图表会有所帮助，但我在网上看到的那些通常包含太多参数或权重和偏差而无用，我的思绪迷失在路径中。}

我刚刚开始在Coursera 上学习 Andrew Ng的机器学习课程.第三周的主题是逻辑回归,所以我试图实现以下成本函数.

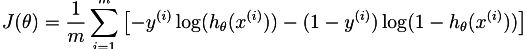
该假设定义为:

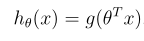
其中g是sigmoid函数:

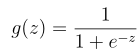
这就是我的功能当前的样子:

function [J, grad] = costFunction(theta, X, y)

m = length(y); % number of training examples
S = 0;
J = 0;

for i=1:m
    Yi = y(i);
    Xi = X(i,:);
    H = sigmoid(transpose(theta).*Xi);
    S = S + ((-Yi)*log(H)-((1-Yi)*log(1-H)));
end

J = S/m;

end

给出以下值

X = [magic(3) ; magic(3)];
y = [1 0 1 0 1 0]';
[j g] = costFunction([0 1 0]', X, y)

j返回0.6931 2.6067 0.6931,即使结果应为j = 2.6067.我假设Xi有问题,但我看不出错误.

如果有人能指出我正确的方向,我将非常感激.

我是Apache Spark的新手,并尝试使用机器学习库来预测一些数据.我现在的数据集只有大约350个点.以下是其中的7个点:

"365","4",41401.387,5330569
"364","3",51517.886,5946290
"363","2",55059.838,6097388
"362","1",43780.977,5304694
"361","7",46447.196,5471836
"360","6",50656.121,5849862
"359","5",44494.476,5460289

这是我的代码:

def parsePoint(line):
    split = map(sanitize, line.split(','))
    rev = split.pop(-2)
    return LabeledPoint(rev, split)

def sanitize(value):
    return float(value.strip('"'))

parsedData = textFile.map(parsePoint)
model = LinearRegressionWithSGD.train(parsedData, iterations=10)

print model.predict(parsedData.first().features)

预测是完全疯狂的,就像-6.92840330273e+136.如果我没有设置迭代train(),那么我得到nan结果.我究竟做错了什么？是我的数据集(可能是它的大小？)还是我的配置？