相关疑难解决方法(0)

众所周知,应用函子在组合下是封闭的,但是monad不是.但是,我一直难以找到一个具体的反例,表明monad并不总是构成.

这个答案给出[String -> a]了一个非monad的例子.在玩了一下之后,我直觉地相信它,但是这个答案只是说"加入无法实现"而没有给出任何理由.我想要更正式的东西.当然有很多类型的函数[String -> [String -> a]] -> [String -> a]; 必须表明任何这样的功能必然不符合monad法则.

任何例子(附带证据)都可以; 我不一定特别想要证明上述例子.

我已经阅读了这篇文章,但最后一节并未理解.

作者说Monad给了我们上下文敏感性,但是只使用Applicative实例就可以实现相同的结果:

let maybeAge = (\futureYear birthYear -> if futureYear < birthYear
    then yearDiff birthYear futureYear
    else yearDiff futureYear birthYear) <$> (readMay futureYearString) <*> (readMay birthYearString)

没有do语法肯定会更加丑陋,但除此之外我不明白为什么我们需要Monad.任何人都可以为我清除这个吗？

Set,类似于[]具有完美定义的monadic操作.问题是它们要求值满足Ord约束,因此不可能定义return并且>>=没有任何约束.同样的问题适用于需要对可能值进行某种约束的许多其他数据结构.

标准技巧(在haskell-cafe帖子中向我建议)是包含Set在延续monad中.ContT并不关心底层类型仿函数是否有任何约束.只有在将Sets 包装/展开到continuation中时才需要约束:

import Control.Monad.Cont
import Data.Foldable (foldrM)
import Data.Set

setReturn :: a -> Set a
setReturn = singleton

setBind :: (Ord b) => Set a -> (a -> Set b) -> Set b
setBind set f = foldl' (\s -> union s . f) empty set

type SetM r a = ContT r Set a

fromSet :: (Ord r) => Set a …

monad是一种数学结构,大量用于(纯)函数式编程,基本上是Haskell.然而,还有许多其他数学结构可用,例如应用函子,强单子或幺半群.有些更具体,有些更通用.然而,monads更受欢迎.这是为什么？

我提出的一个解释是,它们是通用性和特异性之间的最佳点.这意味着monad捕获关于数据的足够假设,以应用我们通常使用的算法以及我们通常满足monadic定律的数据.

另一种解释可能是Haskell为monad(do-notation)提供了语法,但没有为其他结构提供语法,这意味着Haskell程序员(以及函数式编程研究人员)直观地被用于monad,其中更通用或特定(高效)的函数将也工作.

一个最近的问题通常问Haskell的各种类之间的边界.我提出了Handler一个有效的例子,Functor没有合理的Apply**实例,其中

class Functor f => Apply f where
  (<.>) :: f (a -> b) -> f a -> f b
  -- optional bits omitted.

但是,我还没有找到一个Functor无法成为有效(如果无意义)实例的有效示例Apply.这一事实Apply 已经过(见更新),但单行法,

(.) <$> u <.> v <.> w = u <.> (v <.> w)

似乎使这个相当棘手.

pigworker(康纳·麦克布莱德)前面举了一个例子的Functor,是不是Applicative,但他依靠pure这样做,这不是可用Apply.

**后来我意识到实际上可能有一个明智的(虽然有点奇怪)Apply实例Handler,从概念上收集同时异常.

更新

Edward Kmett现在接受 …

什么是约束类型？

为什么有人会使用它(在实践中)？

到底有什么好处呢？

您能举一个简单的代码示例来说明前两个问题的答案吗？

例如,为什么在此代码中使用它？

我非常喜欢Haskell新手,如果答案很明显,我很抱歉,但我正在通过Typeclassopedia努力更好地理解类别.在为Functors部分做练习时,我遇到了这个问题:

举一个类型* - >*的例子,它不能成为Functor的一个实例(不使用undefined).

我的第一个想法是定义某种无限递归的fmap定义,但这undefined与定义中使用的那个基本上不一样吗？

如果有人能够解释答案,我将不胜感激.

谢谢!

原创练习的来源,第3部分:http://www.haskell.org/haskellwiki/Typeclassopedia#Introduction

这个问题来自于一个应用而非Monad的仿函数的例子中的答案 :它声称是

data PoE a = Empty | Pair a a deriving (Functor,Eq)

不能有monad实例,但我没有看到:

instance Applicative PoE where
    pure x = Pair x x
    Pair f g <*> Pair x y = Pair (f x) (g y)
    _        <*> _        = Empty
instance Monad PoE where
    Empty    >>= _ = Empty
    Pair x y >>= f = case (f x, f y) of 
                       (Pair x' _,Pair _ y') -> Pair x' y'
                       _ -> Empty

实际的原因,我相信这是一个单子是,它是同构于Maybe (Pair …

有Functor没有Applicatives的好例子？好的,我正在寻找Const Void不需要诉求的非平凡(不)的例子undefined.如果没有,是否有任何方法可以证明那里的空间无趣？

这类似于不是Functor/Functor/Applicative/Monad的好例子？,但那里没有完全解决.

作为一个后续问题,是否有任何有趣的例子Functor可能会Applicative因为太多的非规范Applicative实例有意义而没有实例？例如,"扩展Maybe"有点无聊

data MayB a = Jus a | Nothing1 | Nothing2 | Nothing3 | ...

instance Applicative MayB where
  pure = Jus
  Jus f <*> Jus x = Jus (f x)
  Jus f <*> n     = n
  n     <*> Jus x = n
  n1    <*> n2    = methodOfResolvingNothingWhatsoever n1 n2

是否存在实例变体Applicative更具实质性的示例？

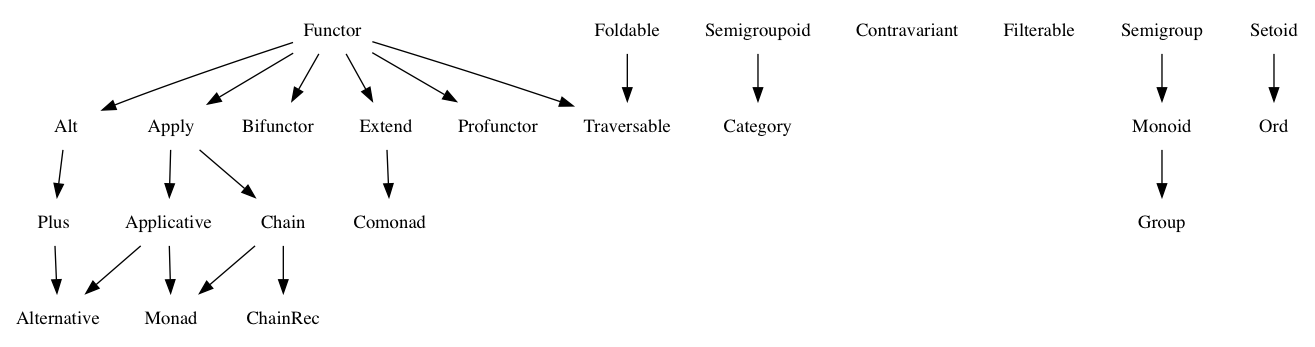
我仍然熟悉所有这些类别理论的东西,而且我看到的每个例子都是使用Maybe或Array.但我没有找到任何区分这些类别的例子.例如,以下是我仍然无法回答的一些问题:

1. 什么是一个不是Monoid的半群？
2. 什么是可折叠的,也不是可穿越的？[重复]
3. 什么是不是也适用的Functor？
4. 什么是申请也不是申请人？
5. 什么是申请,也不是链？
6. 什么链子不是Monad？
7. 什么是不是Monad的申请人？[重复]

我正在通过JavaScript FantasyLand的上下文学习这些东西,这就是我从中获取术语的地方 - 我知道这些东西有不同的词.