相关疑难解决方法(0)
不是Functor/Functor/Applicative/Monad的好例子?
在向某人解释什么是类型类X时,我很难找到正好是X的数据结构的好例子.
所以,我请求示例:
- 一个不是Functor的类型构造函数.
- 一个类型构造函数,它是一个Functor,但不是Applicative.
- 一个类型构造函数,它是Applicative,但不是Monad.
- Monad的类型构造函数.
我认为Monad到处都有很多例子,但Monad的一个很好的例子与之前的例子有一些关系可以完成图片.
我寻找彼此相似的示例,区别仅在于属于特定类型类的重要方面.
如果有人能够设法在这个层次结构的某个地方隐藏一个Arrow的例子(它是在Applicative和Monad之间吗?),那也会很棒!
202
推荐指数
推荐指数
5
解决办法
解决办法
1万
查看次数
查看次数
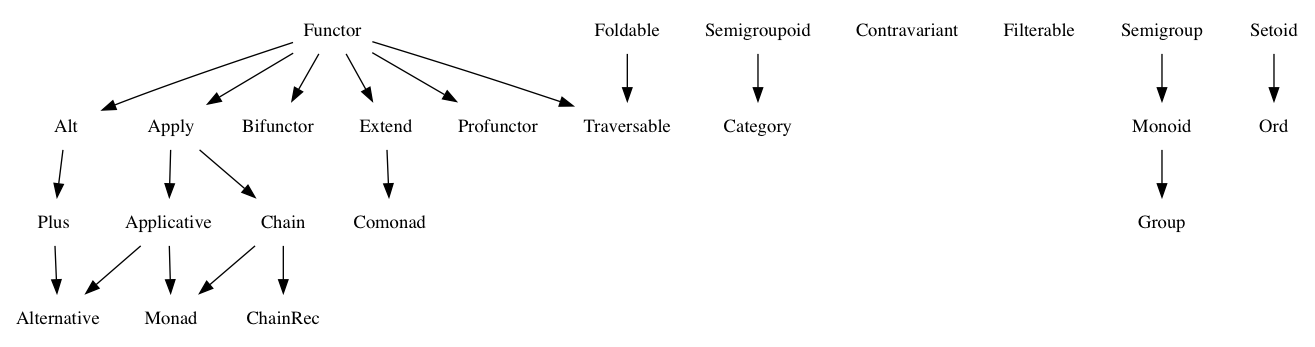
哪些类型可以区分类别?
我仍然熟悉所有这些类别理论的东西,而且我看到的每个例子都是使用Maybe或Array.但我没有找到任何区分这些类别的例子.例如,以下是我仍然无法回答的一些问题:
- 什么是一个不是Monoid的半群?
- 什么是可折叠的,也不是可穿越的?[重复]
- 什么是不是也适用的Functor?
- 什么是申请也不是申请人?
- 什么是申请,也不是链?
- 什么链子不是Monad?
- 什么是不是Monad的申请人?[重复]
我正在通过JavaScript FantasyLand的上下文学习这些东西,这就是我从中获取术语的地方 - 我知道这些东西有不同的词.
12
推荐指数
推荐指数
2
解决办法
解决办法
223
查看次数
查看次数
具体类型无法成为应用程序的Functor示例?
来自不适用的仿函数:
一个类型构造函数,它是一个Functor但不是Applicative.一个简单的例子是一对:
Run Code Online (Sandbox Code Playgroud)instance Functor ((,) r) where fmap f (x,y) = (x, f y)但是如何在
Applicative不对其施加额外限制的情况下定义其实例是没有办法的r.特别是,没有办法如何定义pure :: a -> (r, a)任意的r.
在这里,pure不能同时为所有类型定义; 但是,对于任何具体类型T,人们都可以((,) T)申请.
问题:是否有一个具体仿函数的例子(即,没有涉及类型变量)是一个仿函数而不是一个应用程序?
7
推荐指数
推荐指数
1
解决办法
解决办法
284
查看次数
查看次数