1/BigInteger in c#

Question

我要实现

BigInteger.ModPow(1/BigInteger, 2,5);

但1/BigInteger总是返回0,导致结果也是0如此.我试着BigDecimal为c#寻找一些课程,但我什么都没发现.即使没有,有什么方法可以算这个BigDecimal吗？

Answer 1

1/a| a |> 1为0,因为BigIntegers使用整数除法,其中忽略除法的小数部分.我不确定你对此有何期待.

我假设您想要模数的a模乘法逆m,而不是分数.这个逆存在iff a并且m是共同素数,即gcd(a, m) = 1.

链接的维基百科页面列出了用于计算模乘法逆的两种标准算法:

扩展欧几里德算法,适用于任意模数
它速度快,但具有依赖于输入的运行时.

我手头没有C#代码,但是从维基百科移植伪代码应该是直截了当的.
使用欧拉定理:
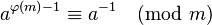
$i ^ { - 1} = i ^ {φ(n)-1}$
这需要知道φ(m),即你需要知道m的素因子.当m它是素数时它是一个受欢迎的选择,因此当它变成时,φ(m)= m-1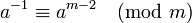 $a ^ { - 1} = a ^ {p-2}$ .如果你需要恒定的运行时间,你知道φ(m),这就是你要走的路.

在C#中,这变成了 BigInteger.ModPow(a, phiOfM-1, m)