解决XKCD中的NP完全问题

Question

问题/漫画有问题:http://xkcd.com/287/

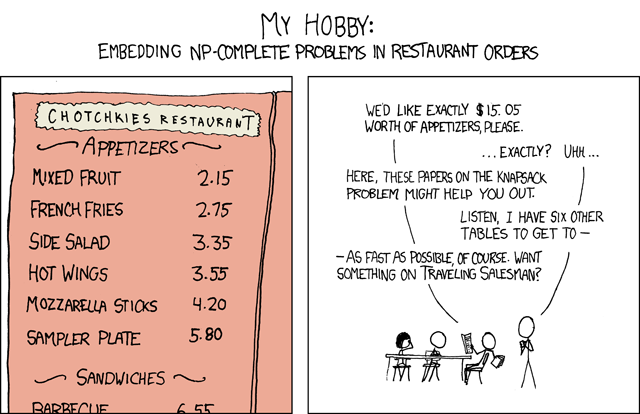
我不确定这是最好的方法,但这是我到目前为止所提出的.我正在使用CFML,但任何人都应该可读.

<cffunction name="testCombo" returntype="boolean">
    <cfargument name="currentCombo" type="string" required="true" />
    <cfargument name="currentTotal" type="numeric" required="true" />
    <cfargument name="apps" type="array" required="true" />

    <cfset var a = 0 />
    <cfset var found = false />

    <cfloop from="1" to="#arrayLen(arguments.apps)#" index="a">
        <cfset arguments.currentCombo = listAppend(arguments.currentCombo, arguments.apps[a].name) />
        <cfset arguments.currentTotal = arguments.currentTotal + arguments.apps[a].cost />
        <cfif arguments.currentTotal eq 15.05>
            <!--- print current combo --->
            <cfoutput><strong>#arguments.currentCombo# = 15.05</strong></cfoutput><br />
            <cfreturn true />
        <cfelseif arguments.currentTotal gt 15.05>
            <cfoutput>#arguments.currentCombo# > 15.05 (aborting)</cfoutput><br />
            <cfreturn false />
        <cfelse>
            <!--- less than 15.05 --->
            <cfoutput>#arguments.currentCombo# < 15.05 (traversing)</cfoutput><br />
            <cfset found = testCombo(arguments.currentCombo, arguments.currentTotal, arguments.apps) />
        </cfif>
    </cfloop>
</cffunction>

<cfset mf = {name="Mixed Fruit", cost=2.15} />
<cfset ff = {name="French Fries", cost=2.75} />
<cfset ss = {name="side salad", cost=3.35} />
<cfset hw = {name="hot wings", cost=3.55} />
<cfset ms = {name="moz sticks", cost=4.20} />
<cfset sp = {name="sampler plate", cost=5.80} />
<cfset apps = [ mf, ff, ss, hw, ms, sp ] />

<cfloop from="1" to="6" index="b">
    <cfoutput>#testCombo(apps[b].name, apps[b].cost, apps)#</cfoutput>
</cfloop>

上面的代码告诉我,最多15.05美元的组合是7个混合水果订单,我需要完成我的testCombo函数的232次执行.

是否有更好的算法来找到正确的解决方案？我找到了正确的解决方案吗？

Answer 1

它给出了解决方案的所有排列,但我认为我在为代码大小击败其他所有人.

item(X) :- member(X,[215, 275, 335, 355, 420, 580]).
solution([X|Y], Z) :- item(X), plus(S, X, Z), Z >= 0, solution(Y, S).
solution([], 0).

使用swiprolog解决方案:

?- solution(X, 1505).

X = [215, 215, 215, 215, 215, 215, 215] ;

X = [215, 355, 355, 580] ;

X = [215, 355, 580, 355] ;

X = [215, 580, 355, 355] ;

X = [355, 215, 355, 580] ;

X = [355, 215, 580, 355] ;

X = [355, 355, 215, 580] ;

X = [355, 355, 580, 215] ;

X = [355, 580, 215, 355] ;

X = [355, 580, 355, 215] ;

X = [580, 215, 355, 355] ;

X = [580, 355, 215, 355] ;

X = [580, 355, 355, 215] ;

No

Answer 2

关于NP完全问题的观点并不是它在小数据集上很棘手,而是解决它的工作量以大于多项式的速率增长,即没有O(n ^ x)算法.

如果时间复杂度为O(n!),如(我相信)上面提到的两个问题,那就是NP.

Answer 3

递归(在Perl中)不是更优雅吗？

#!/usr/bin/perl
use strict;
use warnings;

my @weights  = (2.15, 2.75, 3.35, 3.55, 4.20, 5.80);

my $total = 0;
my @order = ();

iterate($total, @order);

sub iterate
{
    my ($total, @order) = @_;
    foreach my $w (@weights)
    {
        if ($total+$w == 15.05)
        {
            print join (', ', (@order, $w)), "\n";
        }
        if ($total+$w < 15.05)
        {
            iterate($total+$w, (@order, $w));
        }
    }
}

产量

marco@unimatrix-01:~$ ./xkcd-knapsack.pl
2.15, 2.15, 2.15, 2.15, 2.15, 2.15, 2.15
2.15, 3.55, 3.55, 5.8
2.15, 3.55, 5.8, 3.55
2.15, 5.8, 3.55, 3.55
3.55, 2.15, 3.55, 5.8
3.55, 2.15, 5.8, 3.55
3.55, 3.55, 2.15, 5.8
3.55, 5.8, 2.15, 3.55
5.8, 2.15, 3.55, 3.55
5.8, 3.55, 2.15, 3.55

Answer 4

虽然背包是NP Complete,但它是一个非常特殊的问题:它通常的动态程序实际上非常出色(http://en.wikipedia.org/wiki/Knapsack_problem)

如果你做了正确的分析,结果是O(nW),n是项目数,W是目标数.问题是当你必须DP超过大W时,就是当我们得到NP行为时.但是在大多数情况下,背包的表现相当好,你可以毫无问题地解决它的大型实例.就NP完全问题而言,背包是最容易的问题之一.