什么是解决8拼图问题的有效方法?
Pal*_*Dot 18 puzzle algorithm logic a-star sliding-tile-puzzle
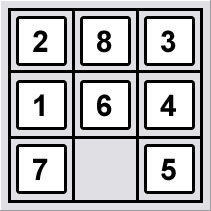
8拼图是一个有9个位置的方板,由8个编号的瓷砖和一个间隙填充.在任何时候,与间隙相邻的瓦片可以移动到间隙中,从而产生新的间隙位置.换句话说,间隙可以与相邻(水平和垂直)瓦片交换.游戏中的目标是从任意配置的瓷砖开始,然后移动它们以便按升序排列编号的瓷砖,或者在电路板的周边运行,或者从左到右排序,左上角为1 - 手的位置.
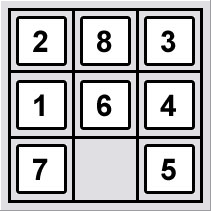
我想知道什么方法可以有效地解决这个问题?
ldo*_*dog 15
我将尝试重写之前的答案,详细说明为什么它是最优的.
直接取自维基百科的A*算法是
function A*(start,goal)
closedset := the empty set // The set of nodes already evaluated.
openset := set containing the initial node // The set of tentative nodes to be evaluated.
came_from := the empty map // The map of navigated nodes.
g_score[start] := 0 // Distance from start along optimal path.
h_score[start] := heuristic_estimate_of_distance(start, goal)
f_score[start] := h_score[start] // Estimated total distance from start to goal through y.
while openset is not empty
x := the node in openset having the lowest f_score[] value
if x = goal
return reconstruct_path(came_from, came_from[goal])
remove x from openset
add x to closedset
foreach y in neighbor_nodes(x)
if y in closedset
continue
tentative_g_score := g_score[x] + dist_between(x,y)
if y not in openset
add y to openset
tentative_is_better := true
elseif tentative_g_score < g_score[y]
tentative_is_better := true
else
tentative_is_better := false
if tentative_is_better = true
came_from[y] := x
g_score[y] := tentative_g_score
h_score[y] := heuristic_estimate_of_distance(y, goal)
f_score[y] := g_score[y] + h_score[y]
return failure
function reconstruct_path(came_from, current_node)
if came_from[current_node] is set
p = reconstruct_path(came_from, came_from[current_node])
return (p + current_node)
else
return current_node
所以让我在这里填写所有细节.
heuristic_estimate_of_distance是函数Σd(x i)其中d(.)是每个平方x i与其目标状态的曼哈顿距离.
所以设置
1 2 3
4 7 6
8 5
将得到heuristic_estimate_of_distance1 + 2 + 1 = 4,因为8,5中的每一个都离他们的目标位置一个,其中d(.)= 1并且7离目标状态为2,d(7)= 2.
A*搜索到的节点集被定义为起始位置,后跟所有可能的合法位置.那就是说起始位置x如上:
x =
1 2 3
4 7 6
8 5
然后该函数neighbor_nodes(x)产生2个可能的合法动作:
1 2 3
4 7
8 5 6
or
1 2 3
4 7 6
8 5
该函数dist_between(x,y)被定义为平方移动所发生转变从状态数x到y.对于算法而言,这总是等于A*中的1.
closedset并且openset都是A*算法专用的,并且可以使用标准数据结构(我相信优先级队列)来实现.这came_from是一个数据结构,用于重建使用reconstruct_path可以在维基百科上找到详细信息的函数找到的解决方案.如果您不想记住解决方案,则无需实现此功能.
最后,我将讨论最优性问题.考虑一下A*维基百科文章的摘录:
"如果启发函数h是可接受的,意味着它永远不会高估达到目标的实际最低成本,那么如果我们不使用闭集,则A*本身是可接受的(或最优的).如果使用闭集,则h也必须是单调的(或一致的)A*才是最优的.这意味着对于任何一对相邻节点x和y,其中d(x,y)表示它们之间边缘的长度,我们必须:h (x)<= d(x,y)+ h(y)"
因此,足以表明我们的启发式是可接受的和单调的.对于前者(可容许性),请注意,给定任何配置,我们的启发式(所有距离的总和)估计每个方格不受合法移动的约束,并且可以自由地朝向其目标位置移动,这显然是乐观估计,因此我们的启发式是否可以接受(或者它永远不会过度估计,因为到达目标位置将始终至少采用与启发式估计一样多的移动.)
单词中所述的单调性要求是:"任何节点的启发式成本(到达目标状态的估计距离)必须小于或等于转换到任何相邻节点的成本加上该节点的启发式成本."
主要是为了防止负循环的可能性,其中转换到不相关的节点可能比实际进行转换的成本减少到目标节点的距离,这表明启发式差.
为了显示单调性,在我们的案例中它非常简单.根据我们对d的定义,任何相邻节点x,y的d(x,y)= 1.因此我们需要表明
h(x)<= h(y)+ 1
这相当于
h(x) - h(y)<= 1
这相当于
Σd(x i) - Σd(y i)<= 1
这相当于
Σd(x i) - d(y i)<= 1
我们通过我们的定义知道neighbor_nodes(x)两个相邻节点x,y最多可以有一个不同的正方形的位置,这意味着在我们的总和中
d(x i) - d(y i)= 0
除了i的1之外的所有值.让我们说,不失一般性,这是i = k.此外,我们知道,对于i = k,节点最多移动了一个位置,因此它到目标状态的距离必须最多比前一个状态多一个:
Σd(x i) - d(y i)= d(x k) - d(y k)<= 1
表现出单调性.这显示了需要显示的内容,从而证明这种算法是最优的(以大O符号或渐近的方式).
请注意,我已经在big-O表示法方面表现出最佳性,但在调整启发式方面仍有很大的发挥空间.你可以添加额外的扭曲,以便更接近目标状态的实际距离,但是你必须确保启发式总是低估,否则你会失去最优性!
稍后编辑了许多月亮
稍后再读这篇文章,我意识到我写它的方式有点混淆了这种算法最优性的含义.
我试图在这里得到两种不同的最优性意义:
1)算法产生最优解,这是给定客观标准的最佳解决方案.
2)该算法使用相同的启发式扩展所有可能算法的最少数量的状态节点.
理解为什么需要启发式的可接受性和单调性以获得1)的最简单方法是将A*视为Dijkstra的最短路径算法在图形上的应用,其中边缘权重由到目前为止的节点距离加上启发式给出距离.如果没有这两个属性,我们在图中会有负边,因此负循环是可能的,Dijkstra的最短路径算法将不再返回正确的答案!(构建一个简单的例子来说服自己.)
2)实际上很难理解.为了完全理解这个含义,这个陈述中有很多量词,例如在谈论其他算法时,一个将similar算法称为A*,它扩展节点并在没有先验信息的情况下进行搜索(除了启发式算法).显然,人们可以构建一个琐碎的反例,否则,例如oracle或genie,它会告诉你每一步的答案.为了深入理解这一陈述,我强烈建议阅读维基百科历史部分的最后一段,并查看该精心陈述的句子中的所有引文和脚注.
我希望这可以清除潜在读者之间的任何混淆.
ldo*_*dog 11
您可以使用基于数字位置的启发式算法,即每个字母距其目标状态的所有距离的总和越高,启发式值越高.然后你可以实现A*搜索,它可以被证明是时间和空间复杂性方面的最佳搜索(假设启发式是单调的和可接受的.)http://en.wikipedia.org/wiki/A*_search_algorithm
- 这个答案措辞的方式给人一种强烈的印象,即它以最佳方式产生最佳答案.但它甚至没有试图做任何启发式适用的论点. (4认同)
- @Jason Orendorff:那是因为这确实在大O符号(渐近行为)方面产生了最好的答案.你可以继续尝试进一步减少运行时间的启发式算法(通过常数因子),但它仍然是你将无法产生更好的渐近时间. (2认同)
| 归档时间: |
|
| 查看次数: |
31025 次 |
| 最近记录: |