使用互相关比较2个信号时,什么是"好的"R值？

Question

我为提前有点冗长而道歉:如果你想跳过所有背景mumbo jumbo,你可以在下面看到我的问题.

这几乎是我之前发布的关于如何比较两个1D(时间相关)信号的问题的后续问题.我得到的答案之一是使用互相关函数(MATLAB中的xcorr),我做了.

背景资料

也许一些背景信息将是有用的:我正在尝试实现独立分量分析算法.我的一个非正式测试是(1)通过以下方法创建测试用例:(a)生成2个随机向量(1x1000),(b)将向量组合成2x1000矩阵(称为"S"),并将其乘以2x2混合矩阵(称为"A"),给我一个新的矩阵(让我们称之为"T").

总之:T = A*S.

(2)然后我运行ICA算法生成混合矩阵的逆(称为"W"),(3)将"T"乘以"W"(希望)给我一个原始信号矩阵的重建(称为"X")

总之:X = W*T.

(4)我现在要比较"S"和"X".虽然"S"和"X"是2×1000,我简单地比较S(1,:),以X(1,:)和S(2,:)对X(2,:)每个都是1x1000的,使他们1D信号.(我还有另一个步骤,确保这些矢量是相互比较的合适矢量,我也将信号归一化).

所以,我现在的困惑是如何"品位"如何接近S(1,:)火柴X(1,:),并同样与S(2,:)对X(2,:).

到目前为止,我使用过类似的东西: r1 = max(abs(xcorr(S(1,:), X(1,:)))

我的问题

假设使用互相关函数是比较两个信号的相似性的有效方法,那么什么被认为是对信号相似性进行分级的良好R值？维基百科说这是一个非常主观的领域,所以我推迟对那些可能在这个领域有经验的人做出更好的判断.

正如你可能已经意识到的那样,我根本不是来自EE/DSP /统计背景(我是一名医科学生),所以我现在正经历一场"火灾洗礼",我很欣赏所有的我可以得到帮助.谢谢!

Answer 1

(编辑:就直接回答有关R值的问题,见下文)

解决这个问题的一种方法是使用互相关.请记住,您必须对幅度进行归一化并校正延迟:如果您有信号S1,并且信号S2的形状相同,但幅度减半并延迟3个样本,它们仍然完全相关.

例如:

>> t = 0:0.001:1;
>> y = @(t) sin(10*t).*exp(-10*t).*(t > 0);
>> S1 = y(t);
>> S2 = 0.4*y(t-0.1);
>> plot(t,S1,t,S2);

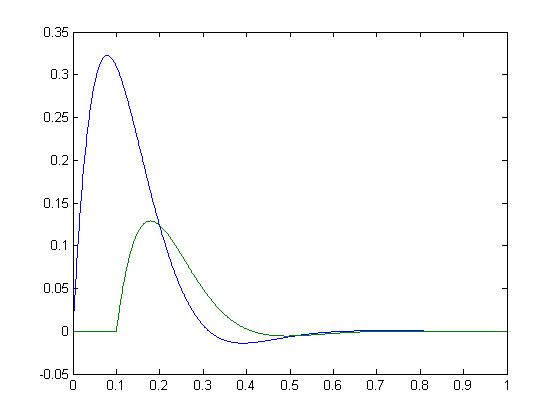
这些应具有完美的相关系数.计算此方法的一种方法是使用最大互相关:

>> f = @(S1,S2) max(xcorr(S1,S2));

f = 

    @(S1,S2) max(xcorr(S1,S2))

>>  disp(f(S1,S1)); disp(f(S2,S2)); disp(f(S1,S2));
   12.5000

    2.0000

    5.0000

xcorr()处理信号之间的时间延迟的最大值.就校正幅度而言,您可以对信号进行标准化,使其自相关性为1.0,或者您可以将该等效步骤折叠为以下内容:

ρ ² = F(S1,S2)² /(F(S1,S1)*F(S2,S2);

在这种情况下ρ ² = 5×5 /(12.5*2)= 1.0

你可以求解ρ本身,即ρ= f(S1,S2)/ sqrt(f(S1,S1)*f(S2,S2)),请记住1.0和-1.0都是完全相关的(-1.0)有相反的迹象)

试试你的信号!

关于接受/拒绝使用的阈值,这实际上取决于您拥有的信号类型.0.9及以上版本相当不错,但可能会产生误导.我会考虑在减去相关版本后查看剩余信号.您可以通过查看xcorr()的最大值的时间索引来执行此操作:

>> t = 0:0.001:1;
>> y = @(a,t) sin(a*t).*exp(-a*t).*(t > 0);
>> S1=y(10,t);
>> S2=0.4*y(9,t-0.1);
>> f(S1,S2)/sqrt(f(S1,S1)*f(S2,S2))

ans =

    0.9959

对于相关性来说,这看起来非常好.但是让我们尝试使用S1的缩放/移位倍数来拟合S2:

>> [A,i]=max(xcorr(S1,S2)); tshift = i-length(S1);
>> S2fit = zeros(size(S2)); S2fit(1-tshift:end) = A/f(S1,S1)*S1(1:end+tshift);
>> plot(t,[S2; S2fit]); % fit S2 using S1 as a basis

>> plot(t,[S2-S2fit]);  % residual

剩余有一些能量; 为了感受多少,你可以使用这个:

>> S2res=S2-S2fit;
>> dot(S2res,S2res)/dot(S2,S2)

ans =

    0.0081

>> sqrt(dot(S2res,S2res)/dot(S2,S2))

ans =

    0.0900

这表示残差具有原始信号S2的能量的约0.81%(均方根振幅的9%).(1D信号与其自身的点积将始终等于该信号与其自身的互相关的最大值.)

我不认为有一个银弹来回答两个信号彼此之间的相似之处,但希望我已经给了你一些可能适合你情况的想法.