如何确定Delaunay三角形是内部还是外部？

Question

我正在编写一个程序,需要实现Medial Axis提取,其中Delaunay三角测量是一个步骤.外部中轴是不需要的,因此要删除相应的外部三角形.幸运的是,我遇到了一个包含大量图表的页面,还有一个确定内部和外部Delaunay三角形的方法("基于虚线周长"),但它只是一个提示,没有详细的解释.谁知道算法？

编辑:我忘了提到从闭合多边形的边界采样的初始点,我的目的是确定每个Delaunay三角形是否在多边形内.

Answer 1

这个解决方案假设你有一个数据结构,用CGAL的方式使用"虚拟无限Delaunay顶点"来表示Delaunay三角剖分(详见此处).

想法是找到边界Delaunay边缘:连接两个连续样本点的边缘; 然后通过Delaunay三角剖分"泛滥"以对Delaunay面部进行分类.人们知道无限顶点是外部的,因此只要不跨越边界边界,就可以将其邻居(和邻居的邻居等)分类为外部.如果到达边界边缘,则可以简单地将相邻三角形标记为内部并且类似地继续.

输入:密集采样的一组封闭形状的边界,甚至可以包含孔
输出:形状内部的Voronoi图(形状的中轴近似)

1. 计算你的积分的Delaunay三角剖分
2. 标记连接两个连续采样点的Delaunay边.(参见本文第4-5页,如何在每个Delaunay边缘进行本地测试)
3. 所有分类无限德劳内面临的外部,他们推到一个队列Q.
4. 虽然Q不是空的
   1. 德劳内面对f =来自Q的流行音乐
   2. 对于f的 每个未分类的邻居三角形t
      • 如果标记t和f共享的Delaunay边缘,则将t分类为f的反面
      • 其他分类牛逼同样喜欢˚F
      • 把t推到Q.
5. 对于每个Delaunay边缘e
   • 如果两个相邻的Delaunay三角形d1,d2都被分类为INTERIOR,则输出连接d1和d2的外心的段.

对于像这样的输入

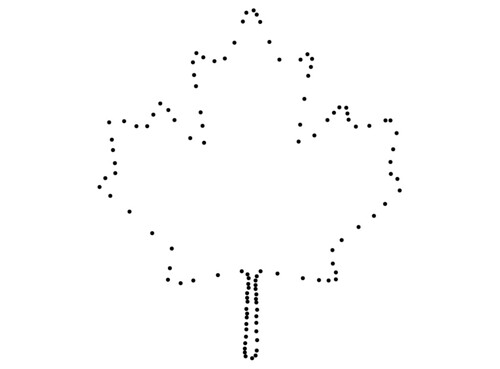
可以计算以下中轴近似值:

您可以使用Mesecina的免费窗口二进制文件检查这个中轴近似在实践中的表现.源代码在这里.