如何构建DAG的biadjacency矩阵?
Han*_*etz 2 graph-theory matrix
对于二分图,您可以将邻接矩阵替换为所谓的biadjacency矩阵:
二部图的邻接矩阵A,其部分具有r和s顶点,具有形式
A = O B
BT O
其中B是r×s矩阵,O是全零矩阵.显然,矩阵B唯一地表示二分图,它通常被称为它的双邻性矩阵.
现在,DAG是一个二分图,例如,您可以在拓扑上对其进行排序,并使U和V集合分别是奇数或偶数拓扑级别的节点.
这意味着,对于具有n个节点的DAG,我只需要(n/2)2矩阵(平均)而不是2矩阵.问题是,我不知道如何构建它.任何提示?
Ore*_*lev 10
我相信你不能为DAG构建一个biadjacency矩阵,因为不是每个DAG都是一个二分图.
这是一个简单的例子:考虑一个有3个顶点的有向图,并将它们表示为A,B和C.边缘连接A到B,B到C和A到C.图形显然是DAG,因为它是定向的并且没有循环(A-> B-> C <-A不是循环).但是,图形不是二分图:没有办法将A,B和C分成两个不相交的集合,其中同一集合中的顶点之间没有边缘.
结论是有图表是DAG而不是二分图,因此不是每个DAG都是二分图.
请注意,您可以在拓扑上对DAG进行排序并将顶点划分为两个不相交的集合,这并不意味着同一集合的顶点之间没有边缘.
似乎A矩阵的biadjacency矩阵B只能在图是无向的时才构造.
基于维基百科的例子:
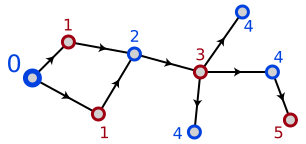
该DAG的邻接矩阵应为:
Blue -> Red
B = 1 1 0 0
0 0 1 0
0 0 0 0
0 0 0 0
0 0 0 1
Red -> Blue
C = 0 1 0 0 0
0 1 0 0 0
0 0 1 1 1
0 0 0 0 0
正如您所看到的,C不是B的转置.似乎无法创建所描述的A矩阵.但是,您可以创建一个这样的A矩阵:
A = 0 B
C 0
这将需要2*(n/2)^ 2空间,其仍然优于n ^ 2.
要构造B和C矩阵,您只需要在U和V(分别)中遍历每个节点以确定出站边缘.
| 归档时间: |
|
| 查看次数: |
1940 次 |
| 最近记录: |