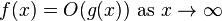大哦:O(n)+ O(n)+ ... + O(n)如何等于O(n ^ 2)？

Question

我很难理解来自S. Dasgupta,CH Papadimitriou和UV Vazirani的算法的以下陈述- 第24页它们代表O(n)之和为O(n ²).但是我对O(n)的理解是n的线性函数,无论线性函数被添加多少次(对于任何给定的n),它都不能是二次的.他们给出了如下的解释,例如13 x 11的二进制表示法.

        1 1 0 1
      x 1 0 1 1
      ----------
        1 1 0 1 (1101 times 1)
      1 1 0 1   (1101 times 1, shifted once)
    0 0 0 0     (1101 times 0, shifted twice)
+ 1 1 0 1       (1101 times 1, shifted thrice)
----------------
1 0 0 0 1 1 1 1 (binary 143)

如果x和y(此处为1101和1011)都是n位,则有n个中间行,长度最多为2n位(考虑到移位).将这些行加起来,一次做两个数字所花费的总时间是O(n)+ O(n)+ ... + O(n),即O(n ²),二次大小为输入.

对不起,如果这是显而易见的,但有人可以帮我理解为什么这是O(n ²)？

Answer 1

如果有n个操作具有O(n)的复杂度,则总复杂度为n ·O(n),即O(n ²).

Answer 2

如果你做的事情需要N秒,并重复N次.完成需要几秒钟？

N = 2 => 2*2 seconds.
N = 3 => 3*3 seconds.
N = 4 => 4*4 seconds.

      => N^2 seconds.

Answer 3

如果O(n)乘以常数因子,那么O(n)不是O(n ²)**.

n is O(n)  
7n is O(n)  
100000n is O(n)

n*n is O(n^2)

以下是来自维基百科的big-O的正式定义:

设f(x)和g(x)是在实数的某个子集上定义的两个函数.一个写道

当且仅当对于足够大的x值,f(x)最多为常数乘以绝对值g(x).即,F(X)= O(G(X))当且仅当存在正的实数M和实数x ₀,使得

**警告:大O是上限.O(n)的所有东西在技术上也是O(n ²).请参阅Big Theta和Big Omega以区别.

http://en.wikipedia.org/wiki/Big_O_notation