为无限和写一个公式,为什么这不能写成?
我在Java中写一个无限的和匹配 -
sqrt(t)*sech(t)^2 dtfrom t=0to t=infinity(无限和从开始t = 0然后结束t = infinity.我正在引用Wolfram Alpha(Mathematica)来比较我的结果).
在更多的数学术语中,这(基本上)是程序正在做的事情.我注意到这是平方(双曲线)割线.虽然,最大值实际上是无限的 -
integrate sqrt(t)*sech(t)^2 dt from t=0 to t=1000
为了匹配这个无限的总和,我在下面写了一个简短的程序.
public class TestSum {
public static void main(String[] args) {
newForm(0.5);
}
public static double newForm(double s) {
int n = 0;
double currentSum = 0;
while (n < 1000) {
double sech = 1 / Math.cosh(n);
double squared = Math.pow(sech, 2);
currentSum = ((Math.pow(n, s))*squared) + currentSum;
if(n == 999)
System.out.println("The current sum is " + currentSum);
n++;
}
return currentSum;
}
}
当我把它插入Mathematica/Wolfram时,我得到 -
integrate sqrt(t)*sech(t)^2 dt from t=0 to t=1000
integral_0^1000 sqrt(t) sech^2(t) dt = 0.758128
运行程序的结果是 -
run:
The current sum is 0.5401365941579325
BUILD SUCCESSFUL (total time: 0 seconds)
我很确定Mathematica没有错.我的计划有什么问题?
您的解决方案不够准确.
积分可以用黎曼和来近似
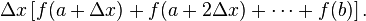
在维基百科上看到Riemann Sum.
delta x(或在你的情况下为delta t)越小,结果越好.
在您的解决方案中delta t = 1,所以近似值并不是很好.
更好地近似结果的可能解决方案是使用:
public class TestSum {
public static void main(String[] args) {
double result= integrate(0, 1000);
System.out.print("result = " + result );
}
public static double integrate(double start, double end) {
double currentIntegralValue = 0;
double dt=0.01d;
double t = start;
while (Math.abs(end - t) >= dt && t-end < 0) {
currentIntegralValue += fn(t)*dt;
t += dt;
}
return currentIntegralValue;
}
private static double fn(double t) {
double sech = 1 / Math.cosh(t);
double squared = Math.pow(sech, 2);
return ((Math.pow(t, 0.5))*squared);
}
}
结果= 0.7579201343666041
您可以使用更小的结果进一步改善结果dt.
dt=0.00001d
结果= 0.7581278135568323
| 归档时间: |
|
| 查看次数: |
1115 次 |
| 最近记录: |