如何计算2D矢量形状的中间轴?
flu*_*lie 4 python svg medial-axis
我将2D形状存储为SVG中的路径元素。形状由贝塞尔曲线和线段组成。
我在使用弧长参数化生成的形状上也有一组等距的点。
如何使用SVG或这些点确定形状的中轴?
我正在使用Python,但是任何形式的伪代码或算法建议都将不胜感激。
以下是我正在处理的形状类型的示例,红色点是沿曲线的采样点。

有点迟,但这里去了:
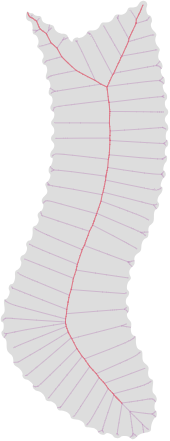
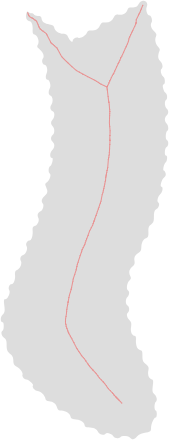
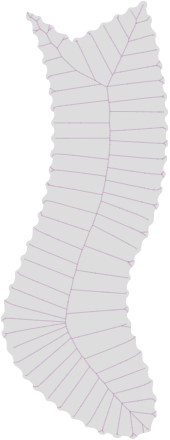


上面的图片显示:(我已经使用在线工具将OP的图像转换为SVG,因此是红点的伪装,即参差不齐的边界)1.叠加了中间和比例轴变换(MAT和SAT)。2.仅缩放轴变换。3.仅中间轴变换。4. 2个分支中的一个(请参阅下文)。5.单三孔的SAT(有许多在MAT)。
为了找到中轴(MA)或中轴变换(MAT)以下算法都可以使用(在上面的图像紫色曲线)(基于一纸 由财,财,月球和嫣-看到一个演示实现这里,也负责处理相交的形状和带有孔的形状)。还存在其他算法。
该算法比查找二进制图像(例如位图)骨架(又名草火或离散变换)要难得多,但是具有一些优势(例如,解析)。为简化起见,下面的讨论仅处理没有孔的简单(不相交)形状的情况。
一些定义
- 曲线 -参数为t的参量贝塞尔曲线。[0,1]。换句话说,矢量图形中使用的典型曲线。
- 形状(?) -(直接取自本文的定义)-“β²中一个连通的有界开放子集的闭环,该子集由有限数量的相互不相交的简单闭合曲线限定”。为了这个答案的目的,可以进一步假定该形状没有孔。简单来说,它是由许多曲线给出的边界所包围的区域-上图中的填充灰色部分。
- 边界 - 形状的边界。换句话说,曲线的索引序列 使得任何曲线在t = 0 的起点都对应于先前曲线在t = 1 的端点。该边界假设积极导向(即通过在逆时针方向沿边界行走形状将永远是你的左边)。
- 边界点 -形状边界上的任何点均由标识曲线和t 曲线参数的索引完全标识。
- 最大磁盘 - 形状内的磁盘也未被该形状内的任何其他磁盘遮挡。每个最大磁盘可以由1个或多个(通常为2个)边界点 s及其中心点标识。
- 正叉 -甲最大磁盘在n个点接触的形状边界相切。
- 分支点 -n == 3 的n叉 最大磁盘中心。换句话说,MA上在MA平面树中形成顶点的点。
- 中间轴(MA) -所有n钉的中心的并集。
- 中间轴变换(MAT) -所有n-prong的并集。换句话说,最大磁盘的半径包括在定义中。
- 接触点(cp) - 链接到 已找到的唯一最大磁盘的边界点。
- 尖角 - 边界点,通常在曲线参数t = 0或 t = 1处,该点不可微分(不平滑),且形成的内角<180°。
- 钝角 -除角度> 180°外,与尖角相同。
- Cp graph-顶点为接触点 s 的图(不一定是平面的),
因此还包含有关所有找到的最大圆盘 s的信息,进而包含
整个MAT的信息。图中的每个顶点(cp)都有以下边缘:
- next-通过沿边界逆时针行走从当前位置找到的第一个接触点。
- prev-通过沿边界顺时针行走从当前触点找到 的第一个接触点。
- next- around-沿逆时针方向绕最大磁盘找到 的第一个接触点。
- prev-around-通过沿顺时针方向绕最大磁盘找到 的第一个接触点。我们可以查看每个上述的作为运算符(。)上的接触点返回另一个接触点通过以下的边缘,例如,如果一个是一个接触点,然后一个。接下来是另一个联系点。
一些注意事项
- 的中轴变换形式的无根平面树树叶在每1-叉中心(包括尖锐拐角或多个); 如果形状有孔,则MAT是平面图。
- 您可以通过对MAT应用比例轴变换(SAT)(上图中的红色曲线)来消除形状边界上的噪声 。该 演示工具这样的变换,基于此 研究。但是,该演示通过确保SAT是MAT的子集来改进算法,并保证拓扑保留。
算法概述
- 找出所有1-prongs ; 它们恰好是中轴树的叶子。这些是尖角和1叉,它们以最大局部向内曲率接触边界点。将1叉的接触点 s 添加到cp-graph。请注意,由于1-prong仅具有一个接触点,因此next-around 和prev-around边缘将再次返回找到的接触点。
- 对于一组代表性的边界点 s(例如OP给出的那些红点),计算其最大圆盘 s。它们通常是2爪子。(请参见下面的“查找2叉”)。通过连接适当的边,将它们的接触点 s 添加到cp图中。请注意,在这种情况下,由于我们发现了2个分支,因此如果遵循next-around (或prev-around)两次,则将返回同一接触点。
最终找到n> = 3 的n个分支。从每个接触点开始:
- 通过从接触点(例如cp1)开始并应用cp1遍历cp图。接下来。反复执行next-around,直到回到cp1为止 。
如果发生上述情况的1或2次迭代,则移至边界 上的下一个接触点(使用next)。但是,如果需要进行3次或更多次迭代,则可以证明存在3个分支的分支点,并且应该在cp1和cp1之间的每个边界块 上插入接触点 s 。接下来。
在这种情况下,请插入3叉(请参见下面的查找方法),然后再次从cp1开始返回步骤1 。
- 重复步骤1和2,直到找到所有3个分支。
- 现在已经隐式地找到了MAT的结构。要提取MAT,需要遍历cp-graph。选择任何 接触点(称为cp1)作为根(为简单起见,假设它链接到2-prong),然后应用下一个(称为cp2)。一条线现在可以得出CP1的链接的最大磁盘 中心到的CP2。这条线是MA的子集的近似值。通过点之间的插值可以获得更好的近似值,因为我们知道了接触点的边界切线。令两个线端点为二次贝塞尔曲线的端点。由于精确地知道了MA在两个最大圆盘中心的方向(通过2个边界切线的平均值),我们在端点处也具有二次贝塞尔曲线的导数,并且我们可以在两点之间构造最佳近似二次贝塞尔曲线。 。如果cp2链接到3叉,则表示MA分支(即分支或分支)形成的平面树,并且我们需要遵循MA的两个 边缘(例如,使用堆栈或递归)。另一方面,如果 cp2链接到1叉MA的叶子已到达,并且该边的遍历停止。实际上,由于MA形成了平面树,因此遍历算法与任何其他树数据结构的遍历算法基本相同。
寻找2叉
我将在这里进行总结,但是Choi等人的论文。很清楚地解释了这一部分,并且易于理解。
在边界上选择一个将成为2叉点的第一个接触点的点,并将其称为bp1。从边界点(即要找到的2叉中的第一个“叉”)绘制一条向内法线 。现在迭代:
- 选择一个点,P1,(在距离D1从BP1沿着该射线)与D1足够大,使得圆(在切线方向绘制BP1 与对射线中心)将切割边界中的至少一个更点。
- 找到最近的边界点到P1,称之为BP2。最后,找到射线上与bp1和bp2等距的点,并将其称为p2。
- 使用新的p1 p2返回步骤2 。
- 重复步骤2和3,直到从p1到两个 边界点 s的距离等于某个公差之内。该2叉现已发现与BP1和BP2它的两个接触点 S和 P1的中心。
寻找三爪
在这里,我们通过构造外接圆而不是使用势函数来偏离本文。
- 选择边界点(cp1)链接的最大磁盘中心作为要找到的3叉中心的初始猜测 。称之为p。
- 找到3最近的点到p seperately到每个3+ 边界片秒。
- 构造这些点的外接圆并将其中心用作新点p。
- 重复步骤2和3,直到从p到3个边界块的距离 等于某个公差之内。
- 将由此找到的3个边界点标记为3 点的接触点。点p是3点的中心。
请随时询问是否不清楚。