C中精度浮点运算的问题
Mic*_*nel 15 c floating-point machine-learning spam-prevention
对于我的课程项目之一,我开始在C中实现"朴素贝叶斯分类器".我的项目是使用大量的训练数据实现文档分类器应用程序(尤其是垃圾邮件).
由于C数据类型的限制,现在我在实现算法时遇到了问题.
(我在这里使用的算法,http://en.wikipedia.org/wiki/Bayesian_spam_filtering)
问题陈述:该算法涉及获取文档中的每个单词并计算它是垃圾词的概率.如果p1,p2 p3 .... pn是字-1,2,3 ... n的概率.使用以下方法计算doc是否为垃圾邮件的概率

这里,概率值可以非常容易地在0.01左右.因此,即使我使用数据类型"double",我的计算也会进行折腾.为了证实这一点,我写了一个给出的示例代码.
#define PROBABILITY_OF_UNLIKELY_SPAM_WORD (0.01)
#define PROBABILITY_OF_MOSTLY_SPAM_WORD (0.99)
int main()
{
int index;
long double numerator = 1.0;
long double denom1 = 1.0, denom2 = 1.0;
long double doc_spam_prob;
/* Simulating FEW unlikely spam words */
for(index = 0; index < 162; index++)
{
numerator = numerator*(long double)PROBABILITY_OF_UNLIKELY_SPAM_WORD;
denom2 = denom2*(long double)PROBABILITY_OF_UNLIKELY_SPAM_WORD;
denom1 = denom1*(long double)(1 - PROBABILITY_OF_UNLIKELY_SPAM_WORD);
}
/* Simulating lot of mostly definite spam words */
for (index = 0; index < 1000; index++)
{
numerator = numerator*(long double)PROBABILITY_OF_MOSTLY_SPAM_WORD;
denom2 = denom2*(long double)PROBABILITY_OF_MOSTLY_SPAM_WORD;
denom1 = denom1*(long double)(1- PROBABILITY_OF_MOSTLY_SPAM_WORD);
}
doc_spam_prob= (numerator/(denom1+denom2));
return 0;
}
我尝试了Float,double甚至是long double数据类型,但仍然存在同样的问题.
因此,在我正在分析的100K字文件中,如果只有162个单词具有1%的垃圾邮件概率而剩余的99838个是明显的垃圾邮件单词,那么我的应用程序仍会因为精度错误而将其称为非垃圾邮件doc(因为分子容易进行)到零)!!!
这是我第一次遇到这样的问题.那么究竟应该如何解决这个问题呢?
Jac*_*cob 19
这通常发生在机器学习中.AFAIK,关于精度的损失你无能为力.因此,为了绕过这一点,我们使用log函数并将除法和乘法转换为减法和加法.
所以我决定做数学,
原始等式是:

我稍微修改一下:
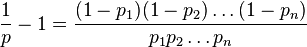
记录两侧的日志:

让,

代,

因此,计算组合概率的替代公式:
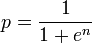
如果您需要我对此进行扩展,请发表评论.
- 当单个'p_i`项非常小时,这仍然会失去一些准确性; 如果这是一个问题,解决方案是将`ln(1 - p_i)`术语替换为`log1p(-p_i)`,它不会遇到同样的问题.(`log1p`是C标准库的未充分利用的宝石) (6认同)
- 使用日志域中的概率几乎是进行计算的唯一合理方法.对数似然比(雅各布答案中的倒数第二个等式)是最简单的形式. (3认同)
- 请注意,在这个特定用法中,它并不重要,因为当`p_i`很小时,`log(p_i)`术语将主导`log(1-p_i)`术语,因此在小的术语对最终结果的影响可以忽略不计.在更一般的用法中,如果你有一个涉及`log(1 + x)`形式的术语的数字敏感计算,你应该考虑用`log1p(x)`替换它. (3认同)
- @Microkernel:谢谢:) - 您可以使用`exp`函数http://www.codecogs.com/reference/c/math.h/exp.php.即使用`exp(eta)`而不是`pow(2.71828182845905,eta)`. (2认同)
- 如果`p_i`的二进制指数是`-n`,那么在计算`log(1-p_i)`时你应该会失去'n-1'位的精度.因此,如果`p_i`是`0.1`(二进制指数:`-3`),那么你可以通过使用`log1p(-p_i)`来保留2位精度.显然这并不是那么糟糕,但如果`p_i`比这小得多,那么损失可能很大.是否值得担心的差异取决于`p_i`s的分布.如果它们都很小并且规模相似,那么它很重要.如果它们的规模差异很大,那可能根本不重要. (2认同)
你的问题是因为你收集了太多的术语而不考虑它们的大小而引起的。一种解决方案是取对数。另一个是对您的个人术语进行排序。首先,我们将方程重写为1/p = 1 + \xe2\x88\x8f((1-p_i)/p_i)。现在你的问题是有些术语很小,而另一些则很大。如果连续有太多小项,就会下溢,如果有太多大项,就会溢出中间结果。
因此,不要连续放置太多相同的订单。对术语进行排序(1-p_i)/p_i。因此,第一个项将是最小的项,最后一个项将是最大的项。现在,如果您立即将它们相乘,您仍然会出现下溢。但计算的顺序并不重要。在临时集合中使用两个迭代器。一个从开头(即(1-p_0)/p_0)开始,另一个从结尾(即(1-p_n)/p_n)开始,中间结果从 开始1.0。现在,当你的中间结果 >=1.0 时,你从前面取一个结果,当你的中间结果 < 1.0 时,你从后面取一个结果。
结果是,当您取项时,中间结果将在 1.0 附近振荡。只有当您用完小项或大项时,它才会上升或下降。但没关系。此时,你已经消耗了两端的极端值,因此中间结果将慢慢接近最终结果。
\n\n当然,确实存在溢出的可能性。如果输入完全不可能是垃圾邮件(p=1E-1000),那么1/p就会溢出,因为\xe2\x88\x8f((1-p_i)/p_i)溢出。但由于项是排序的,我们知道只有溢出时中间结果才会溢出\xe2\x88\x8f((1-p_i)/p_i)。因此,如果中间结果溢出,后续的精度不会损失。
| 归档时间: |
|
| 查看次数: |
1091 次 |
| 最近记录: |