布尔的N间隔规则(C)
Cod*_*key 3 c c++ math integral floating-point-precision
我试图使用这个公式在n个区间内实施Boole的规则 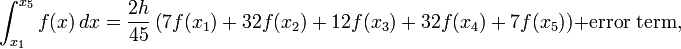

到目前为止我已经开发了这个代码:
//f = function on the range [a,b] n = number of intervals
long double booles(long double (*f) (long double),
double a, double b, int n)
{
long double sum=7*f(a); //because the starting value is not doubled
long double h = (b - a)/(n-1); //width of each interval
int mod;
int i =1;
while (i<n-1)
{
mod = i%4;
if (mod==0)
sum+=14*f(a+i*h);
else if (mod==1)
sum+=32*f(a+i*h);
else if (mod==2)
sum+=12*f(a+i*h);
else
sum+=32*f(a+i*h);
++i;
}
return 2* h/45 * sum;
}
这将运行并给出一个体面的答案,但它不符合Bool的错误规则,该错误表明该错误 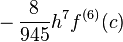 .我修复了第一个术语加倍的问题,但我不确定如何在循环结束时修复可能的加倍.此外,错误相对较大,我不认为我唯一的问题是最后四个术语.
.我修复了第一个术语加倍的问题,但我不确定如何在循环结束时修复可能的加倍.此外,错误相对较大,我不认为我唯一的问题是最后四个术语.
长双
Wiki说:扩展精度浮点类型.实际属性未指定.与float和double类型不同,它可以是80位浮点格式,非IEEE"双倍"或IEEE 754四倍精度浮点格式,如果提供更高精度格式,否则它是相同的双.有关详细信息,请参阅有关long double的文章.
- 所以很难说你实际使用的数据类型(我更喜欢使用双打)
常量
您将整数和浮点数混合在一起,因此编译器必须决定使用什么.重写所有浮动数字,
45以45.0确保它正确完成或a+i*h...i是int并且h是双...积分
不知道值的总和和范围的大小,但为了提高浮动精度,你应该避免将大小值加在一起,因为如果指数太大,你就会失去太多相关的尾数位.
那么两个变量的总和是这样的(在C++中):
Run Code Online (Sandbox Code Playgroud)double suml=0.0,sumh=0.0,summ=1000.0; for (int i=0;i<n;i++) { suml+=...; // here goes the formula if (fabs(suml)>summ) { sumh+=suml; suml=0; } } sumh+=suml; suml=0; // here the result is in sumhsumm是suml的最大值.与您的总和迭代值相比,它应该处于相对安全的范围内,例如100-10000大于平均值的时间.suml是低幅度和变量sumh是大变量和变量
如果你的总和值的范围非常大,那么你可以添加另一个if
Run Code Online (Sandbox Code Playgroud)if (fabs(value)>summ) sumh+=value; else suml+=value;如果它甚至更大,那么你可以以相同的方式对任何变量计数求和,只需将值的范围除以某个意义的全范围
式
可能是我错过了什么,但你为什么要修改?正如我所看到的那样你根本不需要循环而且ifs已经过时了,为什么要使用
a+i*h而不是a+=h?它会提高性能和精度这样的事情:
Run Code Online (Sandbox Code Playgroud)double sum,h; h = (b-a)/double(n-1); sum = 7.0*f(a); a+=h; sum+=32.0*f(a); a+=h; sum+=12.0*f(a); a+=h; sum+=32.0*f(a); a+=h; sum+= 7.0*f(a); a+=h; return 2.0*h*sum/45.0; // + the thing in the bullet 3 of coarse ... // now I see you had an error in your constants !!!
[edit1]划分实施(不是四倍)
//---------------------------------------------------------------------------
double f(double x)
{
// return x+0.2*x*x-0.001*x*x*x+2.0*cos(0.1*x)*tan(0.01*x*x)+25.0;
return x+0.2*x*x-0.001*x*x*x;
}
//---------------------------------------------------------------------------
double integrate_rect(double (*f)(double),double x0,double x1,int n)
{
int i;
double s=0.0,x=x0,dx=(x1-x0)/double(n-1);
for (i=0;i<n;i++,x+=dx) s+=f(x);
return s*dx;
}
//---------------------------------------------------------------------------
double integrate_Boole(double (*f)(double),double x0,double x1,int n)
{
n-=n%5; if (n<5) n=5;
int i;
double s=0.0,x=x0,dx=(x1-x0)/double(n-1);
for (i=0;i<n;i+=5)
{
s+= 7.0*f(x); x+=dx;
s+=32.0*f(x); x+=dx;
s+=12.0*f(x); x+=dx;
s+=32.0*f(x); x+=dx;
s+= 7.0*f(x); x+=dx;
}
s*=(2.0*dx)/(45.0);
return s*1.25; // this is the ratio to cover most cases
}
//---------------------------------------------------------------------------
void main()
{
int n=100000;
double x0=0.0,x1=+100.0,i0,i1;
i0=integrate_rect (f,x0,x1,n); cout << i0 << endl;
i1=integrate_Boole(f,x0,x1,n); cout << i1 << endl << i0/i1;
}
//---------------------------------------------------------------------------
我主要使用矩形规则,因为在FPU上是最快捷,最精确的方式.更高级的方法在纸上更好,但在计算机上增加的开销和舍入通常比矩形规则更慢/更精确
| 归档时间: |
|
| 查看次数: |
1968 次 |
| 最近记录: |