测试一个数字是否是斐波那契

Question

我知道如何制作Fibonacci数列表,但我不知道如何测试给定数字是否属于斐波纳契列表 - 记住的一种方法是生成fib列表.数字达到那个数字并查看它是否属于数组,但必须有另一种更简单,更快速的方法.

有任何想法吗 ？

Answer 1

一个非常好的测试是N是Fibonacci数,当且仅当5 N^2 + 4或是5N^2 – 4一个平方数.关于如何有效地测试数字是正方形的想法请参考SO讨论.

希望这可以帮助

Answer 2

一个正整数,ω是一个Fibonacci数当且仅当一个5ω ²和+ 45ω ² -图4是一个完全平方.

有关更多信息,请参阅Faboulous Fibonacci数字.

Answer 3

虽然有几个人指出了完美的方形解决方案,但它涉及平方斐波纳契数,经常产生大量产品.

少于80个Fibonacci数字甚至可以保存在标准的64位整数中.

这是我的解决方案,其运行完全小于要测试的数量.
(用C#编写,使用类似double和的基本类型long.但算法应该适用于更大的类型.)

static bool IsFib(long T, out long idx)
{
    double root5 = Math.Sqrt(5);
    double phi = (1 + root5) / 2;

    idx    = (long)Math.Floor( Math.Log(T*root5) / Math.Log(phi) + 0.5 );
    long u = (long)Math.Floor( Math.Pow(phi, idx)/root5 + 0.5);

    return (u == T);
}

在我写完这个答案4年多之后,一位评论者询问了第二个参数,并通过了out.

参数#2是Fibonacci序列的"索引".
如果要测试的值T是Fibonacci数,那么idx将是Fibonacci序列中该数字的从1开始的索引.(有一个值得注意的例外)

Fibonacci序列是1 1 2 3 5 8 13,等等
.3是序列中的第4个数字:IsFib(3, out idx);将返回true和值4.
8是序列中的第6个数字:IsFib(8, out idx);将返回true和值6.
13是第7个数字; IsFib(13, out idx);将返回true和重视7.

唯一的例外是IsFib(1, out idx);,2即使值1出现在索引1和2处,它也会返回.

如果IsFib传递非斐波纳契数,它将返回false,并且值idx将是最大斐波那契数小于的索引T.

16不是斐波那契值.
IsFib(16, out idx);将返回false和重视7.
您可以使用Binet的公式将索引7转换为斐波那契值13,这是最小数字小于16.

Answer 4

#!/bin/bash
victim="144"
curl http://aux.planetmath.org/files/objects/7680/fib.txt | sed 's/^[0-9]*//;s/[ \t]//g' | grep "^$victim$" >/dev/null 2>/dev/null
if [[ $? -eq 0 ]] ; then
    echo "$victim is a fibonacci number"
else
    echo "$victim aint"
fi

Answer 5

如果你的数字是有限大小,而不是简单地将所有斐波纳契数字放在上限之下的哈希表中,测试包含就可以了.极少数斐波那契数(例如,仅低于5毫升的38),因为它们呈指数增长.

如果您的数字不是有限大小,那么使用平方测试的建议技巧几乎肯定比生成斐波纳契序列要慢,直到找到或超过该数字.

Answer 6

要找到解决方案,请看看Binet的Formula.
(在维基百科上查找Fibonacci数下的"封闭表达式" )

它说斐波纳契数的序列是由一个简单的闭合公式创建的:

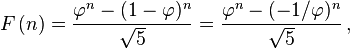
我相信如果你解决n,并测试是否n是一个整数,你会得到你的答案.

编辑为@psmears指出,同一篇维基百科文章也有一节关于检测斐波那契数字.维基百科是一个很好的来源.

Answer 7

正整数ω是斐波那契数

当且仅当一个 5ω ² + 4和5ω ² - 4是完全平方

来自Alfred Posamentier和Ingmar Lehmann的(Fabulous)FIBONACCI编号

bool isFibonacci(int  w)
{
       double X1 = 5 * Math.Pow(w, 2) + 4;
       double X2 = 5 * Math.Pow(w, 2) - 4;

       long X1_sqrt = (long)Math.Sqrt(X1);
       long X2_sqrt = (long)Math.Sqrt(X2);   

       return (X1_sqrt*X1_sqrt == X1) || (X2_sqrt*X2_sqrt == X2) ;
}

我从这个来源复制了它

在1k和之间打印斐波那契数字的片段10k.

for (int i = 1000; i < 10000; i++)
{
         if (isFibonacci(i))
              Console.Write(" "+i);
}

OMG只有四个!

用其他方法

from math import *

phi = 1.61803399
sqrt5 = sqrt(5)

def F(n):
    return int((phi**n - (1-phi)**n) /sqrt5)

def isFibonacci(z):
    return F(int(floor(log(sqrt5*z,phi)+0.5))) == z

print [i for i in range(1000,10000) if isFibonacci(i)]

Answer 8

请参阅维基百科关于Fibonacci数字的文章中的 "识别Fibonacci数"部分.

Answer 9

由于斐波纳契数以指数方式增长,因此您建议的方法非常快.另一个是这个.