查找DAG的所有顶点的可达性计数
Chr*_*isH 7 algorithm graph-theory directed-acyclic-graphs
我试图找到一个具有适度空间要求的快速算法来解决以下问题.
对于DAG的每个顶点,在DAG的传递闭包中找到其in-degree和out-degree的总和.
鉴于此DAG:
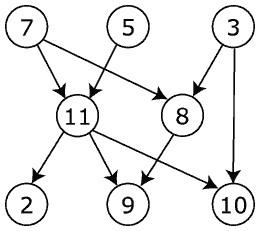
我期待以下结果:
Vertex # Reacability Count Reachable Vertices in closure
7 5 (11, 8, 2, 9, 10)
5 4 (11, 2, 9, 10)
3 3 (8, 9, 10)
11 5 (7, 5, 2, 9, 10)
8 3 (7, 3, 9)
2 3 (7, 5, 11)
9 5 (7, 5, 11, 8, 3)
10 4 (7, 5, 11, 3)
在我看来,这应该是可能的,而不实际构建传递闭包.我无法在网上找到任何确切描述此问题的内容.我有一些关于如何做到这一点的想法,但我想看看SO人群能想出什么.
我已经为这个问题构建了一个可行的解决方案。我的解决方案基于拓扑排序算法的修改。下面的算法仅计算传递闭包中的入度。可以以相同的方式计算出度,其中反转边并将每个顶点的两个计数相加以确定最终的“可达性计数”。
for each vertex V
inCount[V] = inDegree(V) // inDegree() is O(1)
if inCount[V] == 0
pending.addTail(V)
while pending not empty
process(pending.removeHead())
function process(V)
for each edge (V, V2)
predecessors[V2].add(predecessors[V]) // probably O(|predecessors[V]|)
predecessors[V2].add(V)
inCount[V2] -= 1
if inCount[V2] == 0
pending.add(V2)
count[V] = sizeof(predecessors[V]) // store final answer for V
predecessors[V] = EMPTY // save some memory
假设集合操作为 O(1),则该算法的运行时间为 O(|V| + |E|)。然而,集合并运算更有可能使情况predecessors[V2].add(predecessors[V])变得更糟。集合并集所需的附加步骤取决于 DAG 的形状。我相信最坏的情况是 O(|V|^2 + |E|)。在我的测试中,该算法的性能比我迄今为止尝试过的任何其他算法都要好。
此外,通过处理完全处理的顶点的前驱集,该算法通常比大多数替代算法使用更少的内存。然而,上述算法的最坏情况内存消耗确实与构造传递闭包的内存消耗相匹配,但对于大多数 DAG 来说并非如此。
| 归档时间: |
|
| 查看次数: |
3600 次 |
| 最近记录: |