计算3D平面多边形的质心

Question

这是这一个类似的问题一个在这里.

鉴于三维坐标的列表定义面(Point3D1,Point3D2,Point3D3,等),如何计算质心的表面？

在2D中,计算由以下公式给出:

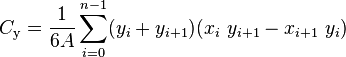
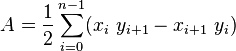
3D模拟怎么样？

Answer 1

只需使用你有两次的公式,但第二次交换中ž为ÿ.

也就是说,计算两个投影的质心,一个投影到xy平面上,另一个投影到xz平面上.投影的质心将是实际质心的投影,因此答案将是您从这两个计算中找到的x,y和z值.

更明确地说明:如果您的点是(x1,y1,z1),(x2,y2,z2),...,要获得xy质心(Cx,Cy),请使用(x1,y1)进行计算, (x2,y2),...并获得xz质心,(Cx,Cz)使用点(x1,z1),(x2,z2),.... - 只需用你的相同的第二次计算2D公式,将z值视为等式中的y.然后你的3D质心将是(Cx,Cy,Cz).只要您的表面是平坦的并且与xy,xz或yz平面不平行(但如果它是平行的,它只是2D方程),这将起作用.

Answer 2

设点为逆时针方向的v ₀ , v ₁ , ..., v _N，其中 v _i = (x _i , y _i , z _i )。

然后三元组 (v ₀ , v ₁ , v ₂ ), (v ₀ , v ₂ , v ₃ ), ..., (v ₀ , v _i , v _i+1 ), ..., (v ₀ , v _N-1 , v _N ) 形成创建多边形的 N-1 个三角形。

每个三角形的面积是| (v _i − v ₀ ) × (v _i+1 − v ₀ ) | ÷ 2，其中 × 是叉积， | · | 是向量长度。

您可能需要将面积设为负值以补偿凹入部分。一个简单的检查是计算(v _i − v ₀ ) × (v _i+1 − v ₀ ) · (v ₁ − v ₀ ) × (v ₂ − v ₀ )。该区域应与结果具有相同的符号。

由于平行投影下二维图形的面积比是恒定的，您可能需要选择一个不平行于平面的单位向量（例如 z），即treat (v _i − v ₀ ) × (v _i+1 − v ₀ ) · z作为面积。有了这个，您不需要执行昂贵的平方根，并且会自动处理符号检查。

每个三角形的质心是(v ₀ + v _i + v _i+1 ) ÷ 3。

因此，整个多边形的质心是，假设密度均匀，

                1       N-1
centroid = ——————————    ?  ( centroid-of-triangle-i × area-of-triangle-i )
           total-area   i=1

（对于尺寸 ? 4D，需要使用 A _i = ½ |v _i -v ₀ | |v _i+1 -v ₀ | sin θ _i计算面积，其中 cos θ _i = (v _i -v ₀ ) · (v _i+1 −v ₀ )。)

Answer 3

如果它是平面，您可以转换为该平面的局部坐标系，使用您提供的公式计算质心，然后转换回来以获得其在 3D 空间中的坐标。