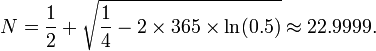为什么我在Python中使用random.shuffle获取重复？

Question

对于10个整数的列表,有10个!可能的订单或排列.为什么random.shuffle仅在5000次尝试后会给出重复项？

>>> L = range(10)
>>> rL = list()
>>> for i in range(5000):
...     random.shuffle(L)
...     rL.append(L[:])
... 
>>> rL = [tuple(e) for e in rL]
>>> len(set(rL))
4997
>>> for i,t in enumerate(rL):
...     if rL.count(t) > 1:
...         print i,t
... 
102 (7, 5, 2, 4, 0, 6, 9, 3, 1, 8)
258 (1, 4, 0, 2, 7, 3, 5, 9, 6, 8)
892 (1, 4, 0, 2, 7, 3, 5, 9, 6, 8)
2878 (7, 5, 2, 4, 0, 6, 9, 3, 1, 8)
4123 (5, 8, 0, 1, 7, 3, 2, 4, 6, 9)
4633 (5, 8, 0, 1, 7, 3, 2, 4, 6, 9)
>>> 10*9*8*7*6*5*4*3*2
3628800
>>> 2**19937 - 1
431542479738816264805523551633791983905393 [snip]

>>> L = list()
>>> for i in range(5000):
...     L.append(random.choice(xrange(3628800)))
... 
>>> len(set(L))
4997

编辑:FWIW,如果一对没有两个相同的概率是:p =(10! - 1)/ 10!并且组合的数量是:C = 5000!/ 4998!*2!= 5000*4999/2然后重复的概率是:

>>> import math
>>> f = math.factorial(10)
>>> p = 1.0*(f-1)/f
>>> C = 5000.0*4999/2
>>> 1 - p**C
0.96806256495611798

Answer 1

它被称为生日悖论.

根据维基百科的这个公式:

但将365与10!您只需要大约2200例有碰撞的可能性为50%,而且你是上面这种方式.

Answer 2

因为它是......随机的!如果你想要所有的排列只需使用itertools.permutations.