如何在函数式编程中实现对内存有效的非破坏性集合操作?
sta*_*ica 20 performance f# functional-programming memory-footprint data-structures
我试图弄清楚如何在函数式编程中实现对大型集合的非破坏性操作,即.如何在不必创建全新集合的情况下更改或删除单个元素,其中所有元素(即使未修改的元素)将在内存中重复.(即使原始集合是垃圾收集的,我也希望这样的集合的内存占用和一般性能很糟糕.)
这是我到目前为止所取得的成就:
使用F#,我想出了一个函数insert,它将列表分成两部分,并在中间引入一个新元素,似乎没有克隆所有未更改的元素:
// return a list without its first n elements:
// (helper function)
let rec skip list n =
if n = 0 then
list
else
match list with
| [] -> []
| x::xs -> skip xs (n-1)
// return only the first n elements of a list:
// (helper function)
let rec take list n =
if n = 0 then
[]
else
match list with
| [] -> []
| x::xs -> x::(take xs (n-1))
// insert a value into a list at the specified zero-based position:
let insert list position value =
(take list position) @ [value] @ (skip list position)
然后,我使用.NET检查来自原始列表的对象是否在新列表中"回收" Object.ReferenceEquals:
open System
let (===) x y =
Object.ReferenceEquals(x, y)
let x = Some(42)
let L = [Some(0); x; Some(43)]
let M = Some(1) |> insert L 1
下面三个表达式所有评估为true,表示该值称为由x两个在列表中被重复使用L和M,即.在内存中只有1个这个值的副本:
L.[1] === x
M.[2] === x
L.[1] === M.[2]
我的问题:
函数式编程语言通常会重用值而不是将它们克隆到新的内存位置,还是我对F#的行为很幸运?假设前者,这是如何在函数式编程中实现合理的内存效率编辑集合?
(顺便说一句:我知道Chris Okasaki的书中的Purely功能数据结构,但还没有时间仔细阅读它.)
Jul*_*iet 28
我试图弄清楚如何在函数式编程中实现对大型集合的非破坏性操作,即.如何在不必创建全新集合的情况下更改或删除单个元素,其中所有元素(即使未修改的元素)将在内存中重复.
该页面有一些F#中数据结构的描述和实现.其中大多数来自Okasaki的纯功能数据结构,尽管AVL树是我自己的实现,因为它没有出现在书中.
现在,既然你问过,关于重用未修改的节点,让我们采用一个简单的二叉树:
type 'a tree =
| Node of 'a tree * 'a * 'a tree
| Nil
let rec insert v = function
| Node(l, x, r) as node ->
if v < x then Node(insert v l, x, r) // reuses x and r
elif v > x then Node(l, x, insert v r) // reuses x and l
else node
| Nil -> Node(Nil, v, Nil)
请注意,我们重用了一些节点.假设我们从这棵树开始:
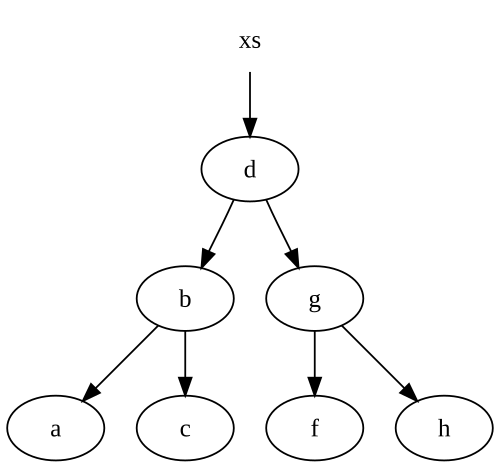
当我们e在树中插入一个时,我们会得到一个全新的树,其中一些节点指向我们原来的树:

如果我们没有在参考xs以上的树,然后将.NET垃圾收集不活动引用任何节点,特别是d,g和f节点.
请注意,我们只修改了插入节点路径上的节点.这在大多数不可变数据结构(包括列表)中非常典型.因此,我们创建的节点数量与我们为了插入数据结构而需要遍历的节点数量完全相同.
函数式编程语言通常会重用值而不是将它们克隆到新的内存位置,还是我对F#的行为很幸运?假设前者,这是如何在函数式编程中实现合理的内存效率编辑集合?
是.
但是,列表不是一个非常好的数据结构,因为对它们的大多数非平凡操作都需要O(n)时间.
平衡二叉树支持O(log n)插入,这意味着我们在每个插入上创建O(log n)副本.由于log 2(10 ^ 15)是〜= 50,因此这些特定数据结构的开销非常小.即使你在插入/删除后保留每个对象的每个副本,你的内存使用率也会以O(n log n)的速率增加 - 在我看来非常合理.
- 哈,在我到达谷底之前,我总能告诉朱丽叶答案.这就像是,"轰!图!" (3认同)
- 确实.我认为特别是`xs`和`ys`树图 - 显示了如何重用大部分分层数据结构 - 帮助我更好地理解不可变数据结构.谢谢你这个非常具有说明性的答案! (2认同)
Nor*_*sey 12
如何在不必创建全新集合的情况下更改或删除单个元素,其中所有元素(甚至是未修改的元素)将在内存中重复.
这是有效的,因为无论哪种集合,元素的指针都与元素本身分开存储.(例外:一些编译器会在某些时候进行优化,但是他们知道他们在做什么.)例如,你可以有两个仅在第一个元素和共享尾部不同的列表:
let shared = ["two", "three", "four"]
let l = "one" :: shared
let l' = "1a" :: shared
这两个列表有shared共同点,它们的第一个元素不同.不太明显的是,每个列表也以唯一的一对开头,通常称为"利弊单元":
List
l以一对包含指针"one"和指向共享尾部的指针开始.List
l'以一对包含指针"1a"和指向共享尾部的指针开始.
如果我们只是声明l并想要改变或删除要获取的第一个元素l',我们会这样做:
let l' = match l with
| _ :: rest -> "1a" :: rest
| [] -> raise (Failure "cannot alter 1st elem of empty list")
有不变的成本:
l通过检查cons细胞分裂成头部和尾部.分配指向
"1a"尾部的新cons单元格.
新的cons单元格成为list的值l'.
如果你在大集合的中间进行类似点的更改,通常你会使用某种使用对数时间和空间的平衡树.您可以较少使用更复杂的数据结构:
Gerard Huet的拉链可以定义几乎任何树状数据结构,并可用于以不变的成本遍历和进行点状修改.拉链很容易理解.
Paterson和Hinze的手指树提供非常复杂的序列表示,其中包括其他技巧使您能够有效地改变中间元素 - 但它们很难理解.
虽然引用的对象在您的代码中是相同的,但我相信引用本身的存储空间,并且列表的结构是重复的take.结果,虽然引用的对象是相同的,并且尾部在两个列表之间共享,但是初始部分的"单元"是重复的.
我不是函数式编程方面的专家,但是对于某种树,你可以实现只复制log(n)元素,因为你只需要重新创建从根到插入元素的路径.
| 归档时间: |
|
| 查看次数: |
945 次 |
| 最近记录: |