如何在JavaScript中计算旋转的3D立方体的x和y坐标？

Question

我试图制作一个3D立方体,由所有单独的小div组成.假设我们有一个3*3*3 div的立方体.关于所有div的事情:

• X,Y,Z坐标(3D立方体)
• 围绕X轴和Y轴的旋转角度

从技术上讲,这应该足以计算立方体的2D透视投影.现在的问题是:我如何计算每个div的X和Y坐标？

PS.此链接的类似示例位于以下链接:http://maettig.com/code/javascript/3d_dots.html.在这个例子中我不喜欢的两件事是:

• 立方体旋转的方式.例如,如果我按下鼠标,立方体就会向上旋转.此外,对于鼠标的水平移动,立方体总是围绕相同的轴旋转,对于鼠标的垂直移动,立方体相对于水平旋转旋转.
• 立方体在角落只有一个"+",我想要一个填充的(大块)立方体.

Answer 1

我认为您提出的问题有两个不同的答案:直接回答您的问题,并回答您的问题:

要"如何计算每个div的X和Y坐标？"

注意 - 以下答案是重新制作我在线程中使用透视投影将GPS点数转换为屏幕点的帖子.您还可以阅读维基百科文章" 3D投影 "以获得更通用的答案.

您需要更多信息来执行透视投影,例如相机/眼睛的位置/方向,视角以及要投影立方体的表面.

有了这一切,你应该能够循环你的div元素,然后在它们的4个角顶点上应用你的旋转变换并投影它们中的每一个,最后使用你得到的2D坐标来渲染元素.

应用旋转

让我们简化一下情况.我们有:

• 顶点A(x_0,y_0,z_0),你的角落之一 div
• θ和δ是定义要应用的旋转的角度,分别为.的俯仰角和偏航角(Tayt-布赖恩角度)

......我们希望:

• D(x,y,z),我们旋转元素的位置

因此,线性化方程是:

• x = sin(?) * y_0 + cos(?) * x_0
• y = sin(?) * z_0 + cos(?) * (cos(?) * y_0 ? sin(?) * x_0)
• z = cos(?) * z_0 i sin(?) * (cos(?) * y_0 ? sin(?) * x_0)

投影 - 介绍

现在我们有:

• 我们的点D(x,y,z)
• w*h,您要投影的曲面的尺寸(innerWidth*innerHeight例如在您的情况下)
• 甲视图的半角 α

......我们希望:

• 表面平面中B的坐标(我们称之为X和Y)

X屏幕坐标的架构:

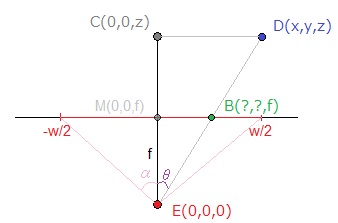
E是我们在这种配置中的"眼睛"的位置,我选择它作为简化的起源.如果不是这种情况和/或如果您还要旋转相机,则需要在下一步之前再次将相应的平移和/或旋转变换应用于D.

可以通过以下方式估计焦距f:

• tan(?) = (w/2) / f (1)

有点几何

您可以在图片上看到三角形ECD和EBM是相似的,因此使用Side-Splitter定理,我们得到:

• MB / CD = EM / EC<=> X / x = f / z (2)

有了(1)和(2),我们现在有:

• X = (x / z) * ( (w / 2) / tan(?) )

注意:Y的推理相同.

实际使用

一些评论:

• 通常,使用α= 45deg,这意味着tan(?) = 1.这就是为什么这个术语在许多实现中都没有出现.

• 如果要保留您显示元素的比例,保持˚F恒定既X和Ÿ,IE的替代计算:

  • X = (x / z) * ( (w / 2) / tan(?) ) 和 Y = (y / z) * ( (h / 2) / tan(?) )

  ......做:

  • X = (x / z) * ( size / 2) / tan(?) )并且Y = (y / z) * ( (size / 2) / tan(?) )使用size您定义的常量值(size = min(w,h)或者size = (w+h)/2经常使用).它只会影响焦点,从而影响视角.

• 正如您在上图中所注意到的,屏幕坐标在此处定义为[-w/2; w/2]对于X和[-h/2; H/2]为Y,但你可能想 [0; w]和 [0; h]相反.X += w/2和Y += h/2-问题解决了.

对于显示由3D制成的3D立方体的问题 div

在我看到这种情况时,上述方法存在缺陷.当然,您可以获得定义旋转和投影div元素的2D坐标,但是如何使用它来渲染它们？.

一旦投影,你div就不会再看起来像矩形,使用简单的CSS很难渲染,特别是如果你的div元素包含复杂的东西.

因此,如果您的真正目的是显示带有旋转和透视的3D DOM立方体,我建议您使用CSS3 3D变换,让浏览器进行计算.

例如,你会在这里找到一个教程来实现只有HTML和CSS3的这种多维数据集.

优点是多方面的:

• 您可以从浏览器GPU加速中受益,使其比使用普通JS更流畅.
• 它影响你的内容div(轮换,perpepective)
• 没有数学要实现

您可能只需要担心针对旧版本的浏览器兼容性(http://caniuse.com/transforms3d).

如果要动态旋转多维数据集(例如,当鼠标移动时),只需使用JS编辑CSS变换

例

我很快就制作了这个JSFiddle,只需从教程中复制实现并添加一个onmousemove处理程序来更新旋转.

希望它有所帮助,再见!